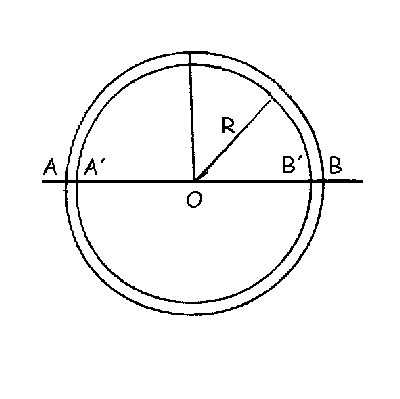
Problema de Propiedades Elásticas de los Sólidos

Un anillo homogéneo de densidad ρ gira en su propio plano alrededor de un eje normal al mismo que pasa por su centro, con una velocidad lineal v. Determinar el esfuerzo de tensión a que está sometido el material del anillo en función de la citada velocidad v. Como aplicación numérica determinar la velocidad máxima a que podrá girar un anillo de hierro de densidad 7.8 g/cm3 si la tensión de rotura es de 4·103 kp/mm2.

σ=v2ρ; vmáx=224.18 m/s

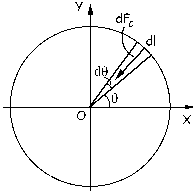Llamaremos dm a la masa correspondiente a un elemento diferencial de longitud dl, tal como vemos en el gráfico.

Por el hecho de estar girando en torno a un eje perpendicular a su plano que pasa por O, ese elemento dm está sometido a la fuerza centrípeta y a la acción que ejercen sobre el mismo los elementos que están junto a él. La fuerza centrípeta será:

Si llamamos V al volumen y S a la sección, la masa del elemento diferencial es:

dm=ρdV=ρSdl=ρSRdθ

La fuerza centrípeta será por tanto:

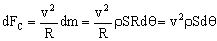
La fuerza centrípeta está dirigida hacia el centro O. Podemos descomponer dicha fuerza en sus dos componentes sobre los ejes cartesianos X e Y:

dFCx=dFCcosθ

dFCy=dFCsenθ

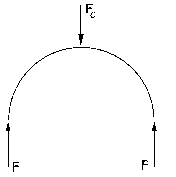Aislamos ahora la mitad del anillo. Tendré que sobre él actúan la fuerza centrípeta y la acción de la mitad del anillo que hemos suprimido. Para esa mitad la componente de la fuerza centrípeta en el eje X es:

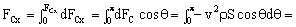
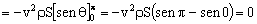
Y en el eje Y:

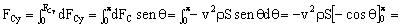
=-v2ρS(-cosπ+cos0)=-2v2ρS

Hemos obtenido por tanto que la fuerza centrípeta neta FC sólo tiene componente Y y vale -2v2ρS. Como el sistema permanece en equilibrio:

ΣFy=0 ⇒ 2F-FC=0 ⇒ 2F-2v2ρS=0 ⇒ F=v2ρS

Y el esfuerzo será:

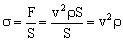
σ=v2ρ

Para trabajar ahora con valores numéricos pasamos todos los datos al Sistema Internacional:

σR=4 · 103 kp/cm2=3.92 · 108 N/m2; ρ=7.8 g/cm3=7800 kg/m3

Las velocidades permitidas serán aquéllas para las cuales el esfuerzo sea inferior al de rotura, es decir:

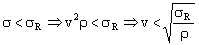
Por tanto si la velocidad debe ser menor que ese valor, la máxima permitida será justo la que nos dé ese valor:

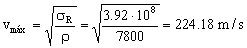
vmáx=224.18 m/s