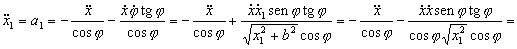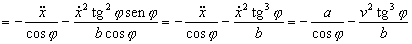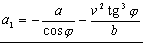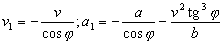
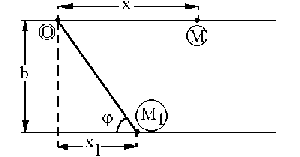
Los puntos M y M1 sólo se desplazan en la dirección del eje X. Llamaremos x a la posición del punto M, y x1 a la posiciòn del punto M1, respecto de un origen fijo O. De este modo, las primeras derivadas respecto del tiempo nos darán las correspondientes velocidades, mientras que las segundas derivadas nos darán las aceleraciónes de estos puntos. Tendremos entonces:
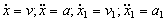
La longitud L de la cuerda que une los puntos M y M1 es constante y podemos expresarla como:
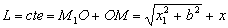
Si derivamos una vez respecto del tiempo:
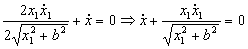
Teniendo en cuenta que:
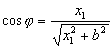
Obtenemos:
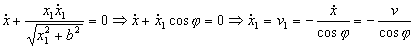
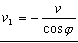
Ahora volvemos a derivar respecto del tiempo:
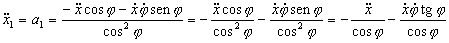
Tenemos que determinar ahora cuánto vale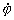 
. Podemos obtenerlo a partir de la expresión del coseno:
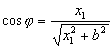
Derivando respecto del tiempo:
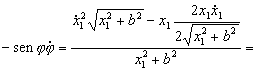
Teniendo en cuenta que:
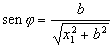
Obtendremos:
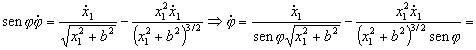
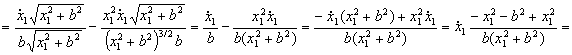
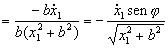
Sustituímos esto en la expresión de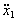 
:
