Problema de Propiedades Elásticas de los Sólidos

Un péndulo de torsión está formado por un alambre de acero ordinario de 80 cm de longitud y 1 mm de diámetro, que lleva en su extremo inferior un disco homogéneo de plomo de 12 cm de diámetro y 1 cm de espesor. Se gira el disco un cierto ángulo y se abandona después, de modo que efectúe oscilaciones de rotación en un plano horizontal. El tiempo empleado en 100 oscilaciones completas es 315 s. a) ¿Qué esfuerzo tensor soporta el alambre? ¿Se supera el límite elástico? b) Calcular la constante de torsión del péndulo c) determinar el módulo de rigidez del acero del alambre. Densidad del plomo: ρPb =11350 kg/m3; límite elástico del acero: 25·107 N/m2.

a) σ=1.60·107 N/m2; no se supera el límite elástico
b) τ=0.00919 Nm
c) G=7.49·1010 N/m2

a) Despreciando el peso del propio alambre, el alambre está sometido al peso del disco. Denominaremos ρd, Vd y rd a la densidad, volumen y radio del disco. La masa del disco será:

md=ρdVd=ρdπrd2hd=11350π·(6·10-2)2·10-2=1.284 kg

Por tanto el esfuerzo, llamando ra al radio del alambre, será:

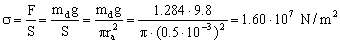
σ=1.60·107 N/m2

Como este esfuerzo es inferior al límite elástico no se supera dicho límite.

NO SUPERA EL LÍMITE ELÁSTICO

 

b) El tiempo empleado en 100 oscilaciones es de 315 s luego el período será:

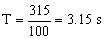
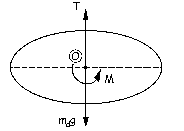Si aislamos el disco, al girarlo un ángulo θ el alambre queda enrollado, proporcionando un momento de sentido opuesto al ángulo girado y proporcional a él. Tomando momentos respecto del centro del disco (que coincide con su centro de masa):

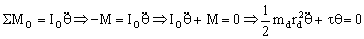
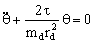
Tenemos la ecuación de un movimiento armónico simple, del tipo:

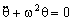
Por comparación la frecuencia angular es:

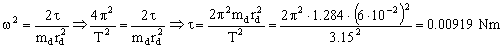
τ=0.00919 Nm

 

b) La constante de torsión del alambre es:

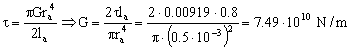
G=7.49·1010 N/m2