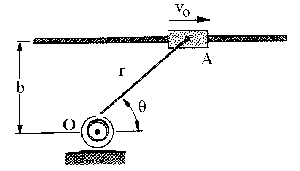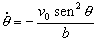
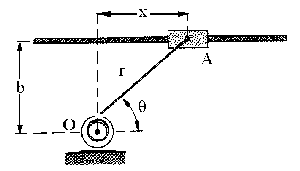
Con respecto al punto fijo O, si llamamos x a la posición en cualquier instante de la deslizadera A (ver figura), su derivada será la velocidad:
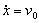
Tendremos entonces del gráfico:
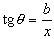
Derivando respecto del tiempo tendremos:
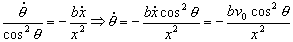
La variable x vale, a partir de la ecuación de la tangente:
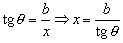
Con lo cual:
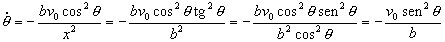
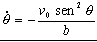
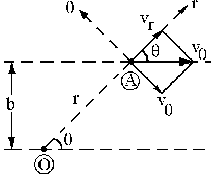
También podemos resolverlo en coordenadas polares. Tendríamos lo que muestra el dibujo para el punto A. En polares tendremos que la velocidad es:
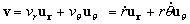
La componente en la dirección de θ será:
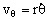
En el gráfico podemos ver que:
vθ =-v0senθ
Sustituyendo vθ por su valor:
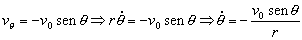
A partir de la expresión del seno podemos calcular r:
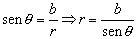
Sustituyendo en la expresión de la derivada de θ :
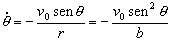
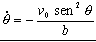
 en función de vo, b y θ.
en función de vo, b y θ.