u=37.62 m/s

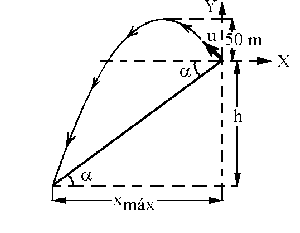
Tomaremos como ejes el eje X horizontal y positivo hacia la derecha y el eje Y vertical y positivo hacia arriba. El ángulo del plano inclinado será:

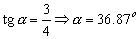
Este ángulo, obviamente no tiene nada que ver con el que forma la velocidad inicial con los ejes.

Tenemos una composición de dos movimientos, uno en el eje X con velocidad uniforme, y otro en el eje Y que será uniformemente acelerado. La velocidad inicial tendrá dos componentes que, de acuerdo a como hemos tomado los ejes, son:

u=-u_xi+u_yj

Para el punto de máxima altura (que llamaremos punto 1) la componente Y de la velocidad será nula. En este eje el movimiento es uniformemente acelerado, y la aceleración es la de la gravedad. Entonces:

v_y1=u_y-gt₁ ⇒ 0=u_y-gt₁ ⇒ u_y=gt₁

Sabemos además que la altura correspondiente a ese punto es de 50 m luego:

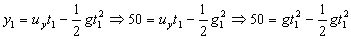
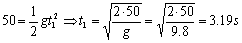
Por tanto la velocidad inicial en el eje Y es:

u_y=gt₁=9.8·3.19=31.3 m/s

Ahora tendremos que la altura que en la figura está marcada como h, es decir, la correspondiente al punto más bajo de la trayectoria, será:

h=250senα =250sen36.87^º=150 m

En ese punto la coordenada x es el alcance máximo:

x_máx=250cosα =250cos36.87^º=200 m

Por tanto tenemos que el punto más bajo de la trayectoria (que llamaremos punto 2) tiene como coordenadas los valores:

x₂=-200 m; y₂=-150 m

Para este punto, si aplicamos las ecuaciones del movimiento al eje Y tendremos:

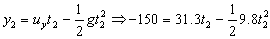
De esta ecuación podemos obtener el tiempo que se tarda en llegar al punto más bajo de la trayectoria:

t₂=9.58 s

Obtenemos en realidad dos soluciones, ya que es una ecuación de segundo grado, pero despreciamos la solución negativa por corresponder con un absurdo. Con este tiempo, la componente X de la velocidad, teniendo en cuenta que en este eje el movimiento es uniforme, es:

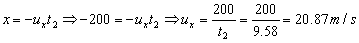
Como la velocidad inicial es un vector de componentes perpendiculares, su módulo será:

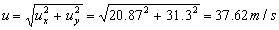
u=37.62 m/s