a) y=0.1sen(300πt-
)
b) 
c) v= 47.12 m/s; a=76925.96 m/s2
d) Δt=0.0067 s
a) Tendremos el sistema que aparece en la figura. La ecuación del movimiento procedente de A es:
yA=AAsen(ωt+kxA)
siendo:
AA=0.4 m; ω=2πν=2π· 150=300π rad/s
Es decir, nos queda la ecuación:
Y la ecuación del movimiento procedente de B será:
yB=ABsen(ωt+kxB)
siendo:
AB=0.3 m; ω=2πν=2π· 150=300π rad/s
Es decir:
El movimiento resultante será del tipo:
y=Asen(ωt+φ)=Asen(300ωt+φ)
Además, por ser la composición de dos movimientos tendré:
y=yA+yB
Sustituyendo por sus correspondientes expresiones:
Desarrollamos los paréntesis, teniendo en cuenta que el seno de una suma es:
sen(a+b)=senacosb+cosasenb
Nos queda:
Igualamos por separado las componentes en los dos ejes, es decir, los términos que llevan cos(300πt) y los términos que llevan sen(300πt):
Simplificamos ambas ecuaciones:
Dividiendo la segunda expresión entre la primera:
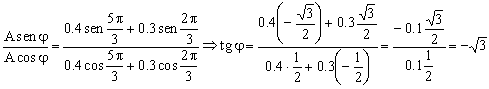
Y la amplitud, a partir de cualquiera de las ecuaciones:
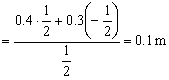
Por tanto la ecuación del movimiento es:
También podemos hacerlo a través del diagrama fasorial. Teniendo en cuenta los desfases tendremos el diagrama que aparece en la figura. Podemos ver fácilmente que los fasores de las dos ondas tienen la misma dirección y sentido contrario, por lo que tendremos que la amplitud resultante A será:
A=AA-AB=0.4-0.3=0.1 m
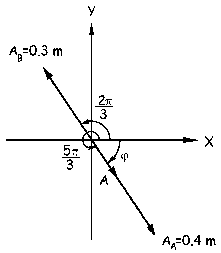Y además, tendrá la dirección del vector mayor, es decir, la dirección de AA. Por tanto:
Y hemos obtenido la misma ecuación de antes, esto es:
b) La intensidad es directamente proporcional al cuadrado de la amplitud. Si representamos por C a esta constante de proporcionalidad tendremos:
La relación de intensidades con respecto al punto A será:
Y respecto al punto B:
c) La velocidad valdrá, derivando la ecuación de la posición respecto del tiempo:
Para t=5 s:
v=47.12 m/s
Y la aceleración, derivando la expresión de la velocidad respecto del tiempo:
Para t=5 s:
a=76925.96 m/s2
d) El tiempo que transcurre entre dos valores iguales de la velocidad tiene que ser el período luego:
Δt=0.0067 s