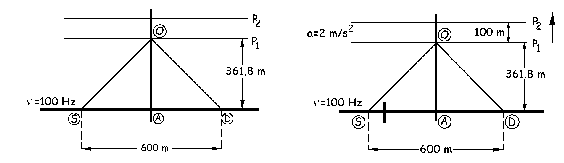a) Δy = 203.53 m
b) ν1= 96 Hz; ν2 = 93.4 Hz
a) En la primera posición P1 de la pared tenemos un mínimo en D. Llamaremos r1 a la distancia recorrida desde S hasta D por el camino directo, y r2 a la distancia recorrida desde S hasta D con la reflexión. Si en D hay un mínimo, el desfase entre las dos ondas que llegan a D debe ser un número impar de veces π. Este desfase, que se debe a la diferencia de caminos recorridos por las dos ondas, es:
![]()
Hemos tenido en cuenta que la reflexión en la pared produce un desfase adicional de π radianes.
En la posición P2 de la pared tenemos otra vez un mínimo. Además, como se han observado entre medias 100 máximos significa que el desfase ha variado 200π. Por tanto, si antes teníamos el mínimo de orden (2n+1) ahora tenemos el mínimo de orden [(2n+1)+200]. Denominaremos ahora r1 al camino directo de la onda, que es el mismo de antes, y r´2 al camino con la reflexión, que será mayor que r2. Tendremos:
![]()
r´2-r1=(n+100)λ
Si restamos las dos expresiones obtenidas:
r´2-r1-r2+r1=(n+100)λ-nλ ⇒ r´2-r2=100λ ⇒ r´2=r2+100λ
La longitud de onda es:
![]()
Y por el teorema de Pitágoras podemos ver que:
![]()
Entonces sustituyendo:
r´2=r2+100λ=940+100 · 3.4=1280 m
Ahora, si llamamos y´ a la distancia AO en la posición P2 e y a la distancia AO en la posición P1 tendremos:
![]()
Por tanto el espacio recorrido por la pared es:
Δy=y´-y=565.33-361.8=203.53 m
Δy=203.53 m
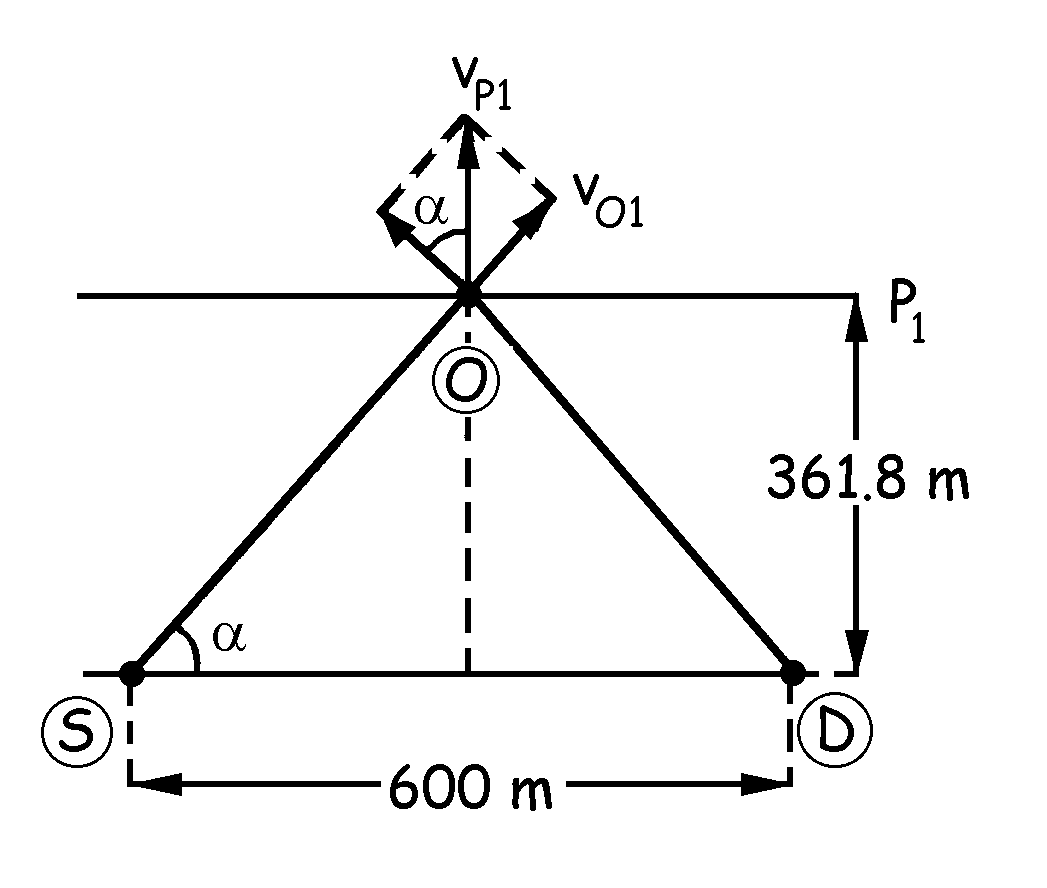 b) En la posición P1 el observador O percibe una frecuencia que será, por el efecto Doppler:
b) En la posición P1 el observador O percibe una frecuencia que será, por el efecto Doppler:
![]()
El observador se aleja y la fuente está en reposo luego nos queda:
![]()
Como tenemos que proyectar las velocidades sobre la recta que une el observador con la fuente necesitamos conocer el ángulo α, que vale:
![]()
Obtenemos entonces:
![]()
 A su vez, el observador O refleja esta onda y es como si fuera una fuente que emitiera una frecuencia ν1 que es percibida por un observador en D como ν´. Ahora la fuente es O y el observador es D, luego tendremos:
A su vez, el observador O refleja esta onda y es como si fuera una fuente que emitiera una frecuencia ν1 que es percibida por un observador en D como ν´. Ahora la fuente es O y el observador es D, luego tendremos:
![]()
Ahora la fuente se aleja y el observador está en reposo luego:
![]()
Sustituyendo la frecuencia ν1 por su valor nos queda:
![]()
![]()
De donde obtenemos la velocidad de la pared en la posición P1:
![]()
Sustituyendo, la frecuencia ν1 percibida por el observador O en la posición P1 es:
![]()
ν1=96 Hz
En la posición P2 la pared se ha desplazado 100 m con movimiento rectilíneo uniformemente acelerado (a=2 m/s2) siendo la velocidad inicial vP1 y la final vP2. Aplicando las ecuaciones del movimiento:
![]()
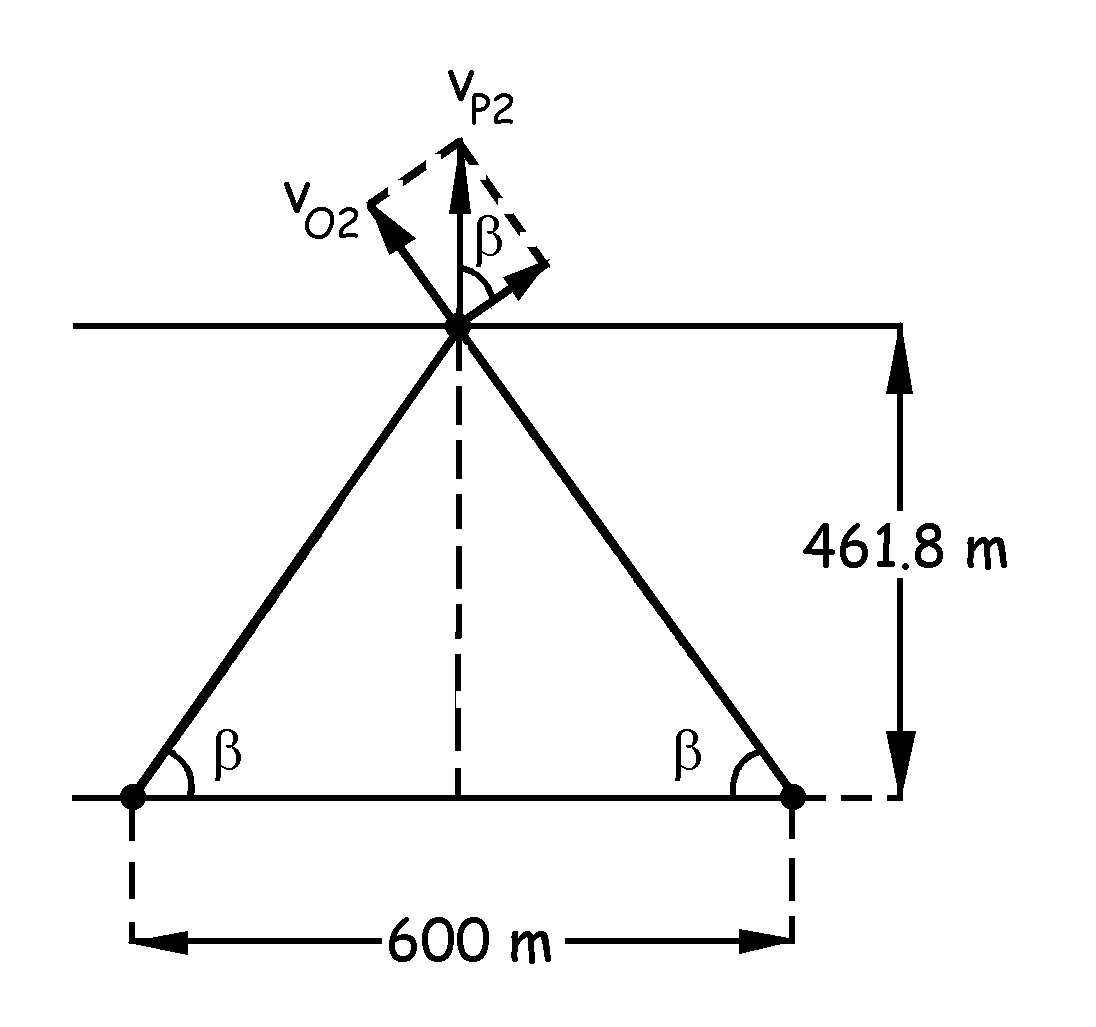 Entonces, en la nueva posición P2 (la pared estará a 361.8+100=461.8 m de la fuente y el detector) tendremos el sistema que aparece en la figura. Para proyectar las velocidades necesitaremos el ángulo β que vale:
Entonces, en la nueva posición P2 (la pared estará a 361.8+100=461.8 m de la fuente y el detector) tendremos el sistema que aparece en la figura. Para proyectar las velocidades necesitaremos el ángulo β que vale:
![]()
Por la ecuación del efecto Doppler tendremos:
![]()
El observador se aleja y la fuente está en reposo luego:
![]()
ν2=93.4 Hz