a) ν = 4250 s-1
b) v = 510 m/s
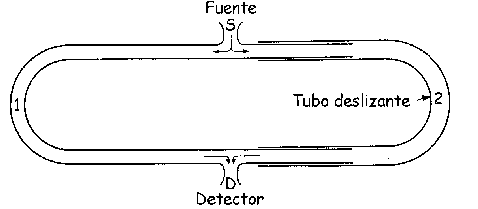
a) Tenemos que en el punto D se producen interferencias porque nos llegan ondas que recorren caminos diferentes, una recorre el tubo 1 y la otra el tubo 2. Para que se produzca un máximo, el desfase tiene que ser un número par de veces π. Este desfase será:
![]()
donde r1 y r2 son los caminos recorridos a través del tubo 1 y del tubo 2 respectivamente. A continuación el tubo 2 se desplaza 2 cm. Como saldrían 2 cm por arriba y otros 2 cm por abajo, tendremos que el nuevo camino recorrido en este tubo es:
r´2=r2+d
siendo d:
d=2 +2=4 cm=0.04 m
El recorrido por el tubo 1 no habrá variado. En estas condiciones se percibe un mínimo en el punto D, luego el desfase entre las dos ondas será ahora un número impar de veces π:
![]()
Si restamos las dos expresiones que hemos obtenido:
![]()
Por tanto la frecuencia:
![]()
ν=4250 s-1
b) Tenemos ahora exactamente lo mismo, sólo que el tubo 2 se desplaza 3 cm, por lo que:
d=3+3=6 cm=0.06 m
Entonces del mismo modo que en el apartado a) obtenemos:
λ=2d=2 · 0.06=0.12 m
Y la velocidad del sonido en el gas:
v=λν=0.12 · 4250=510 m/s
v=510 m/s