a=298.87 nm
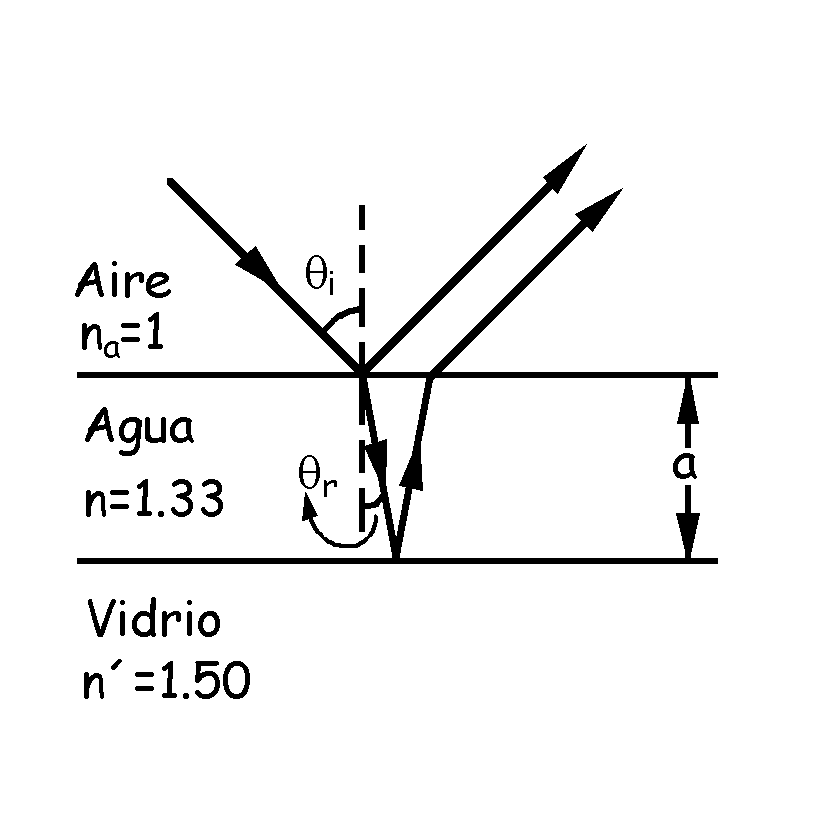Tenemos una lámina delgada tal como aparece en la figura. Se producen interferencias debido a que los rayos reflejados en la cara superior de la lámina y los reflejados en la cara inferior han recorrido caminos diferentes, de modo que tienen un cierto desfase. Para que se observe un mínimo el desfase entre las dos ondas debe ser igual a un número impar de veces π:
δ=(2N+1)π
En el desfase habrá que tener en cuenta tanto la diferencia de caminos como los desfases adicionales de π radianes que producen ciertas reflexiones. En nuestro caso se producen dos desfases de π radianes, uno en la cara superior de la lámina y otro en la cara inferior. Tendremos entonces:
Hemos despreciado el desfase de 2π por ser igual al de 0º y no influir en el resultado final. Como la incidencia es normal:
θi=0º
Aplicando la ley de Snell:
nasenθi=nsenθr ⇒ nasen0º=nsenθr ⇒ 0=nsenθr ⇒ senθr=0 ⇒ θr=0º ⇒ cosθr=cos0º=1
Y nos queda la expresión:
A continuación nos dicen que variando la longitud de onda pasamos a observar un máximo. Llamaremos λ´ a la nueva longitud de onda. Para que se observe un máximo el desfase entre las ondas debe ser un número par de veces π luego nos quedará:
Igual que antes despreciamos el desfase de 2πradianes, y la incidencia es normal, con lo que ya hemos visto que el cosθr=1:
Como el espesor de la película no varía podemos igualar las dos ecuaciones obtenidas:
530N=530 ⇒ N=1
Y ahora sustituimos en una cualquiera de las expresiones que nos dan el espesor de la película:
a=298.87 nm
Podemos comprobar que se obtiene el mismo resultado sustituyendo en la otra expresión:
