Δx=2mm

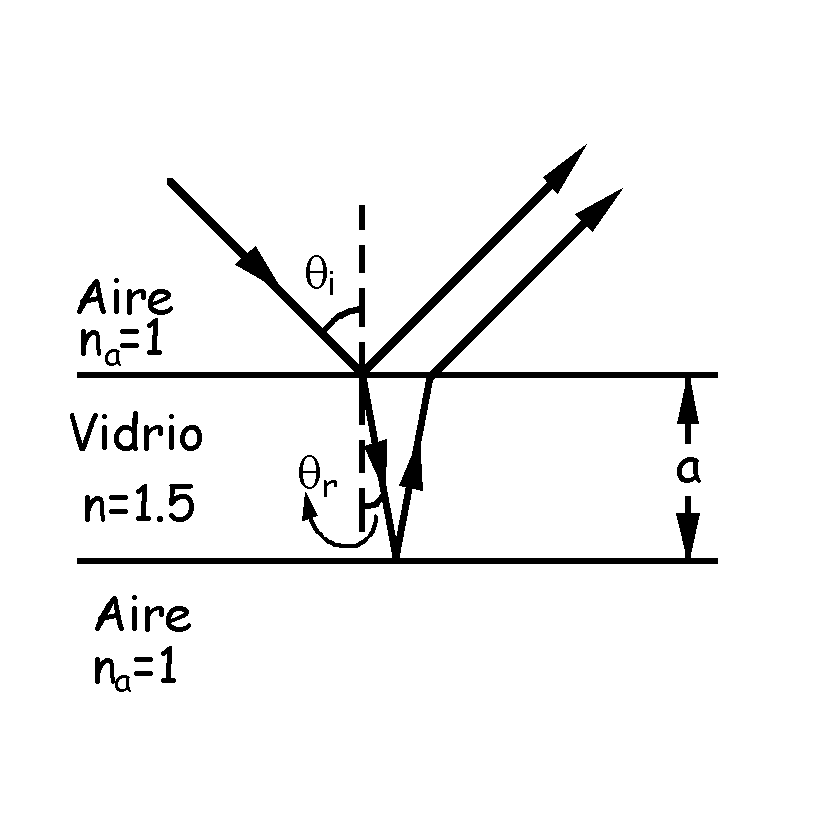Tenemos en este caso una película de vidrio de espesor variable, nulo en el vértice y que crece hacia el extremo. Por otro lado, el fenómeno de las interferencias es el mismo que en cualquier problema de láminas delgadas, produciéndose la interferencia entre ondas que se reflejan en la cara superior de la cuña y ondas que se reflejan en la cara inferior. Por lo demás, lo único que es diferente a otros problemas es la geometría del sistema.

Nos dicen que se observan franjas oscuras, luego debemos aplicar la condición de mínimo, es decir, que el desfase sea igual a un número impar de veces π. En dicho desfase debemos tener en cuenta un desfase adicional de π radianes que se produce en la reflexión en la cara superior de la lámina. Con estos preliminares la condición de mínimo será:

La luz inciden normalmente luego el ángulo de incidencia es nulo. Aplicando la ley de Snell tenemos:

n_asenθ_i=nsenθ_r ⇒ n_asen0º=nsenθ_r ⇒ 0=nsenθ_r ⇒ senθ_r=0 ⇒ θ_r=0º ⇒ cosθ_r=cos0º=1

Nos queda entonces la expresión:

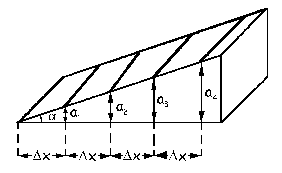Como se ve en esta ecuación, para distintos valores de N crecientes tendremos distintos valores del espesor a crecientes para los cuales aparecerá una banda oscura en la cuña. En primer lugar tenemos que cuando N=0, el espesor correspondiente es nulo, luego tendremos la primera banda oscura en el vértice de la cuña, único punto de la misma de espesor nulo. Vemos la representación de esto en la figura adjunta. Para N=1:

Podemos ver que geométricamente:

Δx=2 mm