r1 =0.1095 cm ; r2=0.1897 cm; r3=0.2449 cm; N=667 anillos
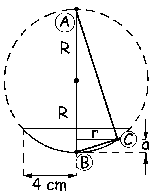Tenemos el sistema que aparece en la figura. Se producen interferencias porque entre la lente y la superficie de apoyo se forma una capa de aire de espesor variable. En función del espesor de esta lámina la interferencia es constructiva o destructiva, apareciendo bandas brillantes u oscuras. Como el espesor de la lámina es igual alrededor de la lente, la forma de estas bandas es circular de radio r, denominándose anillos de Newton. En el problema nos dicen que los anillos son oscuros, es decir, que la interferencia es destructiva. Entonces el desfase tiene que ser igual a un número impar de veces π:
La incidencia es casi normal, lo que implica que el ángulo de incidencia es nulo. Aplicando la ley de Snell:
nsenθi=nsenθr ⇒ nsen0º=nsenθr ⇒ 0=nsenθr ⇒ senθr=0 ⇒ θr=0º ⇒ cosθr=cos0º=1
Sustituyendo:
Además, la lámina que produce la interferencia es de aire, luego el índice de refracción es la unidad (n=1):
Hemos visto ya en los problemas anteriores la relación entre el espesor de la capa de aire y el radio del anillo de Newton:
Sustituyendo:
Para el primer anillo de Newton:
r1=0.1095 cm
Para el segundo anillo:
r2=0.1897 cm
Y para el tercer anillo:
r3=0.2449 cm
El último anillo será aquél cuyo radio sea el más próximo posible al del casquete esférico, es decir, 4 cm. Para dicho anillo, si además se cumple la condición de mínimo:
N debería ser un número entero, lo que implica que el último anillo se formará cuando N=666, cuyo radio será:
Tal como hemos visto la secuencia, si N=666, dicho anillo será el número 667:
667 ANILLOS