Problema de Interferencias

La función de onda estacionaria en una cuerda fija por sus dos extremos es:

y(t, x)=0.3sen(0.01x)cos(200t)

con t en segundos y x e y en cm; a) determinar la amplitud, frecuencia, y velocidad de fase de las ondas progresivas cuya superposición da lugar a esta onda estacionaria; b) escribir las funciones de onda correspondientes a estas ondas progresivas; c) hallar la distancia internodal.

a) A=0.15 cm; ν=31.83 s-1; v=20000 cm/s
b) yi=-0.15 sen(200t-0.01x); yr=0.15sen(200t+0.01x)
c) Δxnodos=314.16 cm

a) Las ondas incidente y reflejada serán del tipo:

yi=Asen(ωt-kx)

yr=-Asen(ωt+kx)

Hemos tenido en cuenta en las ecuaciones que las amplitudes tienen signo contrario, y que ambas ondas se mueven en la misma dirección pero sentido contrario, de modo que hemos cambiado el signo de la x en la reflejada respecto de la incidente.

La suma de estas dos ondas da lugar a la onda estacionaria:

y=yi+yr=Asen(ωt-kx)-Asen(ωt+kx)

Desarrollamos los paréntesis, teniendo en cuenta a qué es igual el seno de una suma y el seno de una diferencia:

sen(a+b)=senacosb+cosasenb

sen(a-b)=senacosb-cosasenb

Nos queda entonces la expresión:

y=Asen(ωt-kx)-Asen(ωt+kx)

y=Asenωtcoskx-Acosωtsenkx-Asenωtcoskx-Acosωtsenkx

y=-2Acosωtsenkx

Comparamos esta onda con la que nos da el enunciado como onda resultante y tenemos:

y=0.3sen(0.01x)cos(200t) ⇒ -2Acosωtsenkx=0.3sen(0.01x)cos(200t)

Tenemos que por comparación:

En módulo:

A=0.15 cm

La frecuencia angular será:

ν=31.83 s-1

Y el número de ondas:

La velocidad de la onda entonces es:

v=20000 cm/s

b) La onda incidente será:

yi=Asen(ωt-kx)=-0.15sen(200t-0.01x)

yi=-0.15sen(200t-0.01x)

Y la onda reflejada:

yr=-Asen(ωt+kx)=0.15sen(200t+0.01x)

yr=0.15sen(200t+0.01x)

 

c) La distancia internodal es de media longitud de onda luego:

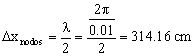
Δxnodos=314.16 cm