ν=456.58 s-1
Pasamos las velocidades al Sistema Internacional:
vF=108 km/h=30 m/s; vW=36 km/h=10 m/s
Y la temperatura:
T=17ºC=290K
Vamos a ver cuánto vale la velocidad del sonido a 17ºC, que son las condiciones del problema. La dependencia de la velocidad con la temperatura es:
![]()
donde ϒ es la constante adiabática del gas, R es la constante de los gases perfectos, T es la temperatura y M es la masa molecular del gas. Para dos temperaturas dadas, por ejemplo, 0ºC y una temperatura T tendremos:
![]()
Dividiendo las dos expresiones:
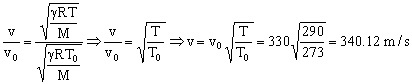
Ahora vamos a calcular la frecuencia a la que emite el móvil. Para un tubo cerrado por un extremo:
![]()
Para el sonido fundamental:
![]()
Como la frecuencia que emite el móvil es 10 veces mayor:
ν=10νT=10 · 42.51=425.1 s-1
 Ahora tenemos el sistema que aparece en la figura. El ángulo α vale:
Ahora tenemos el sistema que aparece en la figura. El ángulo α vale:
![]()
Aplicamos la fórmula del efecto Doppler y tendremos:
![]()
El observador está en reposo y la fuente se acerca luego eligiendo los signos correctos:
![]()
Tenemos que proyectar las velocidades sobre la recta de unión observador-fuente y además en la velocidad de las ondas habrá que tener en cuenta la velocidad del viento, que en este caso favorecerá el movimiento del sonido:
vF=30cosα=30cos36.87º=24 m/s
v=340.12+vWcosα=340.12+10cos36.87º=348.12 m/s
Sustituyendo todo:
![]()
ν´=456.58 s-1