Problema de Interferencias

Un hilo de aluminio de longitud l1=60 cm y sección recta de 10-2 cm2 es soldado a un hilo de acero de la misma sección y longitud l2=86.6 cm. Se fija el hilo así formado sobre la pared y se aplica sobre el extremo libre una tensión de 10 kg. Se producen ondas transversales en el hilo usando una fuente externa de frecuencia variable. a) Calcular la frecuencia más baja para la cual se forman ondas estacionarias de tal forma que la unión de los dos hilos sea un nodo. b) ¿Cuál es el número total de los nodos observados en esta frecuencia excluyendo los dos nodos de los extremos del hilo? ρAl=2.6 g/cm3; ρAcero=7.8 g/cm3</SUP.

a) ν=323.6 s-1
b) n=6

a) Tenemos los datos:

lAl=60 cm=0.6 m; lAc=86.6 cm=0.866 m; SAl=SAc=S=10-2 cm2=10-6 m2; T=10 kg=98 N;

ρAl=2.6 g/cm3=2600 kg/m3; ρAc=7.8 g/cm3=7800 kg/m3

Ambos hilos deben cumplir la condición de ondas estacionarias en una cuerda, que es:

En los dos casos que tenemos, es decir, para el acero y para el aluminio:

La frecuencia es la misma para las dos cuerdas luego:

Hemos llegado a que la relación que tienen que cumplir nAl y nAc es:

nAl=0.4nAc

Además sabemos que estos números tienen que ser enteros. La frecuencia más baja será aquélla para la cual nAl y nAc sean los menores números enteros que cumplen esa relación. Para determinarlos vamos tanteando hasta que encontremos la primera pareja de enteros que verifica la ecuación:

nAc=1 ⇒ nAl=0.4nAc=0.4 · 1=0.4

nAc=2 ⇒ nAl=0.4nAc=0.4 · 2=0.8

nAc=3 ⇒ nAl=0.4nAc=0.4 · 3=1.2

nAc=4 ⇒ nAl=0.4nAc=0.4 · 4=1.6

nAc=5 ⇒ nAl=0.4nAc=0.4 · 5=2.0

Aquí encontramos los primeros enteros válidos. Sustituyendo en una cualquiera de las ecuaciones que nos da la frecuencia:

ν=323.6 s-1

 

b) Para ver el número de nodos que tenemos en el sistema vamos a dibujarlo. Como podemos ver en la ecuación inicial, para que tengamos ondas estacionarias en la cuerda debía cumplirse que:

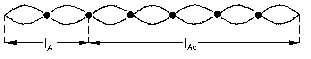En esta ecuación podemos ver que n es el número de semilongitudes de onda que hay en cada cuerda. Tenemos entonces que en el tramo de aluminio hay que poner 2 semilongitudes de onda, y en el tramo de acero debemos poner 5 semilongitudes de onda. Tenemos pues lo que aparece en la figura. Si contamos el número de nodos excluyendo los de los extremos tendremos:

6 NODOS