a) R=11147 km
b) v_B=7901 m/s
c) E_T=-3·10¹⁰ J; L=3.2·10¹³ kgm²/s; T=5065.67 s
d) F=40992 N
e) θ=57.44^o

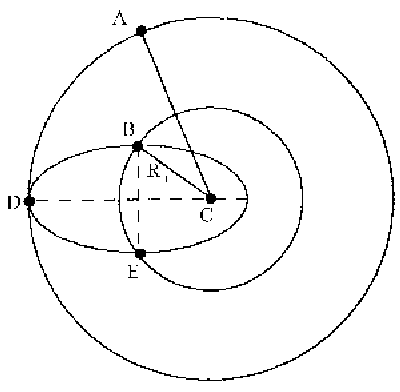
a) Llamaremos M a la masa de la Tierra, R_T a su radio, m_S a la masa de la estación espacial y m_C a la masa de la carga. Tenemos el período de la órbita circular, T_S, correspondiente a la estación espacial: T_S=3 h 15 min 27 s=11727 s. La estación espacial se encuentra en una órbita circular; la única fuerza a que se halla sometida es la de atracción gravitatoria, y la única aceleración que posee es la normal o centrípeta, ya que el movimento en esta órbita es circular y uniforme. Como fuerza y aceleración tienen la misma dirección y sentido, aplicaremos la segunda ley de Newton, con lo que nos queda:

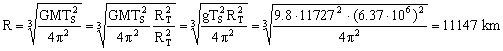
R=11147 km

 

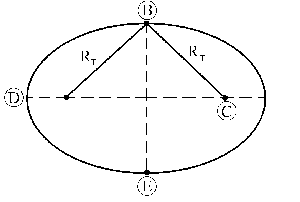b) La carga se encuentra en la órbita elíptica. La elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante e igual a 2a. Hemos dibujado la elipse correspondiente a la carga, que es la que nos interesa ahora. El punto B está colocado sobre el eje menor de la elipse, es decir, en el centro. Si aplicamos la definición de elipse a este punto tendremos que por simetría:

2a=R_T+R_T ⇒ 2a=2R_T ⇒ a=R_T

Ahora, en la órbita elíptica se conserva la energía, luego determinándola en el punto B tendremos:

v_B=7901.01 m/s

 

c) La energía total vale: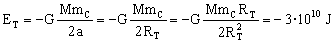

E_T=-3 · 10¹⁰ J

El momento angular es muy difícil determinarlo en el punto B, donde conocemos radio y velocidad, ya que desconocemos el ángulo que forman estos dos vectores. Es más sencillo utilizar el punto D, en el cual la velocidad y el radio vector son perpendiculares, por lo que el momento angular es directamente el producto del radio vector por la cantidad de movimiento (como el ángulo que forman ambos vectores es de 90^º el seno vale la unidad). El momento angular entonces valdría: L=L_D=r_Dm_Cv_D=Rm_Cv_D. Tendremos que determinar lo primero de todo la velocidad en el punto D. Para ello aplicamos la conservación de la energía:

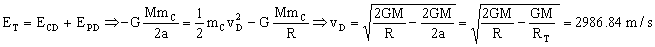
Y el momento angular será: L=Rm_Cv_D=11147 ·10³ · 961 · 2986.84=3.2 · 10¹³ kgm²/s

L= 3.2 · 10¹³ kgm²/s

El período lo determinaremos aplicando la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores, es decir:

T=5065.67 s

 

d) En las proximidades del punto D la fuerza ejercida sobre la carga es tangente a la circunferencia, lo mismo que las velocidades. Como todos los vectores tienen la misma dirección, aplicamos en esta dirección escalarmente el teorema del impulso:

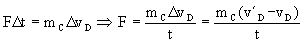siendo v_D y v´_D las velocidades de la carga en las proximidades del punto D antes y después de la aplicación de la fuerza F.

Inmediatamente antes de la aplicación de la fuerza, la carga tiene una velocidad v_D que será la propia de una órbita elíptica, es decir: v_D=2986.84 m/s. Inmediatamente después de la aplicación de la fuerza la carga estaría en la órbita circular de radio R, para la cual:

La fuerza aplicada, por tanto, es:

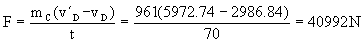
F=40992 N

 

e) Vamos a determinar ahora el ángulo ACD que define la posición de la estación en el momento del lanzamiento de la carga, y que a partir de ahora llamaremos θ. La estación espacial está en una órbita circular, luego en ella la velocidad angular es constante. Tendremos entonces que con esta velocidad angular podemos determinar el ángulo θ. Si llamamos t al tiempo que tarda la estación en ir desde A hasta D tendremos: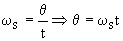

Tenemos que determinar entonces esos dos factores, la velocidad angular de la estación S y el tiempo que tarda en recorrer el ángulo θ. La velocidad angular es sencilla de calcular, ya que como el movimiento es circular y uniforme: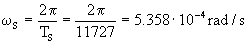

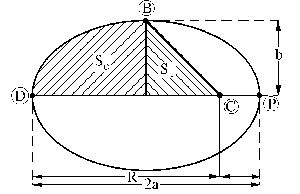El tiempo t es más complicado. Hay que fijarse que la estación y la carga salen a la vez, respectivamente de los puntos A y B, y llegan a la vez al punto D. Por tanto, el tiempo que tarda la estación en ir desde A hasta B debe ser el mismo que el que tarda la carga en ir desde B hasta D. Nos centraremos entonces en la carga. La carga describe una órbita elíptica, en la cual la velocidad areolar es constante. Esto quiere decir que el tiempo empleado en ir de un punto a otro es proporcional al área barrida por el radio vector. Vamos a fijarnos pues en el área que barre el radio vector cuando la carga se desplaza desde B hasta D, que sería el área rayada que aparece en la figura. Fíjate que no es, como a simple vista pudiera parecer, un cuarto de la elipse, sino un cuarto más un triángulo rectángulo. Tendremos que determinar cuánto vale esta área. Llamaremos S_T a la superficie del triángulo, S_C a la del cuarto de elipse, y S₁ a la superficie total barrida por el radio vector, es decir:

Nos falta el eje menor b, que es la media geométrica entre las distancias máxima y mínima. La distancia mínima es:

R_P=2a-r_D=2R_T-R=2·6.37·10⁶-11147·10³=4.777·10⁶ m.

Por tanto el eje menor es:

Con estos datos ya podemos determinar el área S₁ barrido por el radio vector:

Ahora, en la elipse la velocidad areolar es constante, luego tendremos:

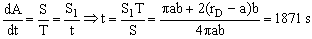
Si volvemos a la ecuación que habíamos planteado al principio para determinar el ángulo θ:

θ=ω_St ⇒  θ=57.44^o