a) f = -25.71 cm; f´=25.71 cm; V1H=2.86 cm; V2H´=-4.28 cm
b) (s´)V2=30 cm; real, invertida y menor
a) En primer lugar debemos determinar los focos correspondientes a cada una de las superficies. Marcaremos con el subíndice 1 a la primera superficie (la de la izquierda) y con el subíndice 2 a la segunda superficie (la de la derecha). Tendremos en cuenta que como las dos superficies son convexas, el radio de la primera será positivo mientras que el radio de la segunda será negativo. Llamaremos además n al índice de refracción de fuera de la varilla, es decir, el índice de refracción del aire (n=1) y n´ al índice de refracción de la varilla (n´=1.5). Tendremos entonces:
![]()
![]()
Nos quedará el sistema como aparece en la figura.
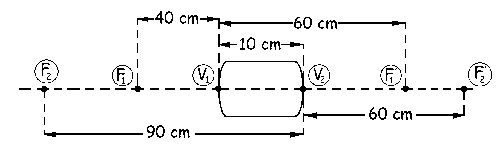
A continuación se debe determinar el intervalo óptico t, que es la distancia desde F´1 hasta F2, considerada positiva si para ir desde F´1 hasta F2 se va hacia la derecha (en el sentido de incidencia de la luz) y negativa si para ir de F´1 a F2 se va hacia la izquierda. Podemos ver en el gráfico que dicho intervalo óptico vale:
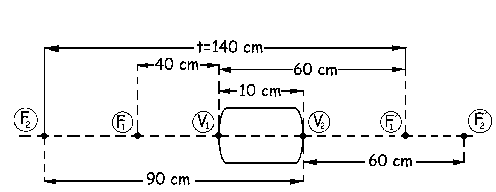
t=F´1F2=-(60+90-10)=-140 cm
Los focos del sistema total serán entonces:
![]()
F=25.71 cm
![]()
F´=25.71 cm
No podemos representar aún estos puntos porque están medidos respecto de los planos principales objeto e imagen, y aún no conocemos las posiciones de estos planos. Las distancias desde los planos principales objeto (H) e imagen (H´) a los vértices son:
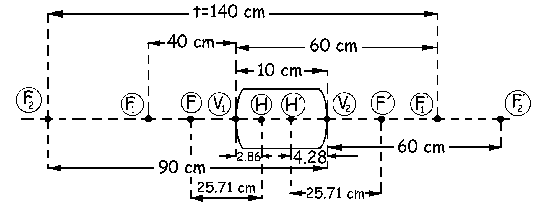
![]()
V1H=2.86 cm
![]()
V2H’=-4.28 cm
El sistema nos queda como aparece en la figura.
b) Ahora tenemos que determinar la imagen de un punto objeto. Con una lente gruesa se trabaja de igual forma que con una delgada, con la diferencia de que hay que medir las distancias objeto respecto del plano principal objeto, y las distancias imagen respecto del plano principal imagen. Por comodidad entonces, trazamos otra figura como la anterior pero en la que únicamente se vean los planos principales y el objeto. La distancia desde el objeto hasta el plano principal objeto (H) podemos ver que es:
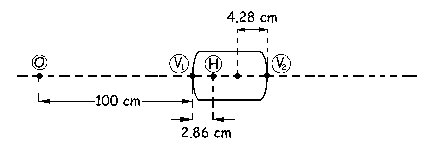
S=-(100+2.86)=-102.86 cm
Aplicando ahora la ecuación de las lentes:
![]()
Esta distancia está medida respecto del plano principal imagen, como puede verse en la figura. Si queremos la distancia desde el borde de la varilla, es decir, desde el vértice V2 tendremos:

(S´)V2=34.28-4.28=30 cm
(S´)V2=30 cm
La distancia imagen es positiva, luego la imagen está a la derecha de la lente. Se habrá formado por los rayos luego es una imagen real.
En cuanto a su tamaño, el aumento lateral, teniendo en cuenta que a ambos lados de la lente hay aire, será:
![]()
Además, este aumento lateral también se define como la relación entre el tamaño de la imagen y el tamaño del objeto, es decir:
![]()
Como β es negativo, eso quiere decir que el signo del numerador y del denominador deben ser necesariamente distintos, lo que implica que la imagen es invertida respecto del objeto.
Además, en módulo, β es inferior a la unidad, luego:
![]()
La imagen es menor que el objeto.
IMAGEN REAL, INVERTIDA Y MENOR