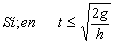
El dardo dará en el blanco si en algún instante de tiempo después de ser disparado el dardo y empezar el blanco a caer, ambos coinciden en el mismo punto (x,y).

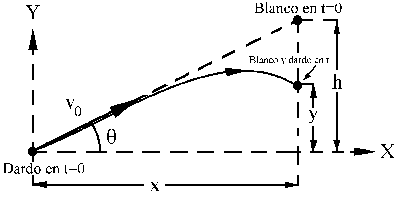
Nos guiaremos para la resolución del problema del esquema adjunto con sus correspondientes ejes. Tendremos que h es la altura del blanco y x es la distancia desde la cervatana. Llamaremos además v₀ a la velocidad inicial del dardo y θ
al ángulo que esta velocidad forma con el eje X. La recta que va desde el dardo en t=0 hasta el blanco en t=0 indicaría cómo se apunta con la cervatana, es decir, directamente tal como se ve en t=0. Denominaremos además t al tiempo que tarda el dardo en llegar al punto (x, y). El dardo dará en el blanco si en ese tiempo t el blanco recorre la distancia h-y.

Para el dardo:

En el eje X tendremos movimiento uniforme, mientras que en el eje Y tendremos movimiento uniformemente acelerado siendo la aceleración la de la gravedad (vertical y hacia abajo). Las velocidades iniciales del dardo son:

v_0x=v_x=cte=v₀cosθ; v_0y=v₀senθ

Durante ese tiempo t el dardo debe recorrer una distancia x. Entonces:

x=v_xt=v₀cosθt

Por tanto el tiempo t vale:

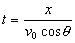
En ese tiempo t, la altura correspondiente al dardo será:

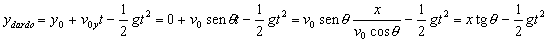
Puede verse en el gráfico que por trigonometría:

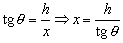
Sustituyendo esto en la expresión correspondiente a la altura del dardo:

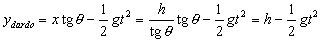
Para ese mismo tiempo t la altura correspondiente al blanco, teniendo en cuenta que el dardo parte con una altura inicial de h y sin velocidad inicial, será:

Como puede verse, en el tiempo t:

y_dardo=y_blanco

Luego el dardo siempre dará en el blanco.

Sí alcanza el blanco.

Para que todo esto tenga sentido físico, tal como hemos elegido los ejes la altura y debe ser positiva, luego:

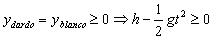
De donde obtenemos: