1º: a) r=2.24 mm; b) f´a=1.70 mm; f´b=2.15 mm
2º: a) l=335.74 mm; b) βob=-40; βoc=31; β=-1249
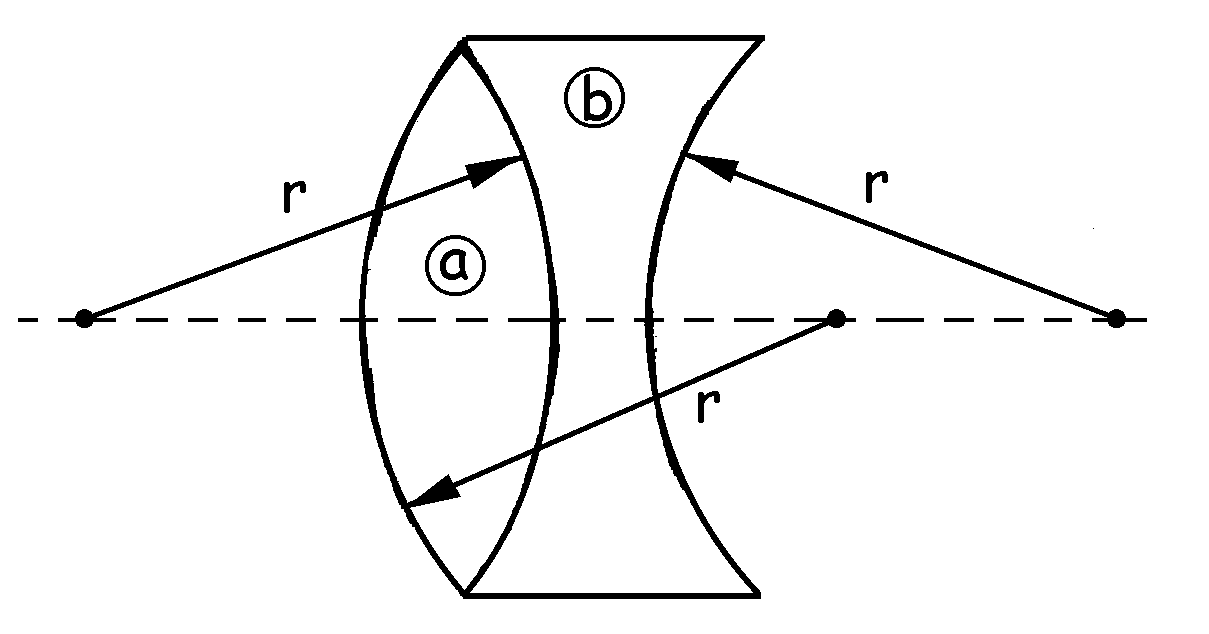 1ºa) El objetivo tiene la forma que aparece en la figura. Denominaremos r al radio de todas las lentes, lente a a la lente biconvexa, y lente b a la lente bicóncava. La potencia del objetivo es:
1ºa) El objetivo tiene la forma que aparece en la figura. Denominaremos r al radio de todas las lentes, lente a a la lente biconvexa, y lente b a la lente bicóncava. La potencia del objetivo es:
![]()
Para la lente a tendremos:
![]()
Y para la lente b:
![]()
Para lentes yuxtapuestas las potencias son aditivas luego:
![]()
r=2.24 mm
1ºb) Ahora para saber la potencia de cada una de las lentes no tenemos más que sustituir:
![]()
f´a=1.70 mm
Y en el otro caso:
![]()
f´b=-2.15 mm
2ºa) La distancia focal del ocular es:
![]()
El microscopio en principio no es más que un sistema formado por dos lentes convergentes consecutivas, el objetivo y el ocular, que actúan una a continuación de la otra. La longitud del microscopio l es la distancia entre el objetivo y el ocular. Sabemos que hay un objeto O situado a 8.2 mm del objetivo y a su izquierda, por lo que la distancia objeto será negativa. Tendremos entonces que para el objetivo:
![]()
La imagen O´ dada por el objetivo está a 328 mm de él y a su derecha. Tendremos lo que aparece en la figura.

En el enunciado nos han dado ya que la imagen final O´´ está a 24 cm (es decir, a 240 mm) del ocular. Para el ocular entonces conocemos la distancia imagen y la focal luego:
![]()
![]()
Podemos ver en el gráfico que la longitud del microscopio es:
![]()
l=335.74 mm
2ºb) El aumento del objetivo, teniendo en cuenta que a ambos lados de esta lente hay aire:
![]()
βOb=-40
Para el ocular, haciendo lo mismo tendremos:
![]()
βOc=31
El aumento comercial del microscopio vale:
![]()
donde Γ es la distancia mínima de visión distinta (25 cm=250 mm en personas normales) y t es el intervalo óptico (distancia desde el foco imagen del objetivo hasta el foco objeto del ocular).
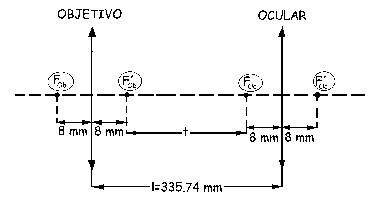
Podemos ver en el gráfico adjunto que el intervalo óptico vale:
t=335.74-8-8=319.74 mm
Con lo cual el aumento comercial del microscopio será:
![]()
β=-1249