f´= 10 cm

Para todo el problema llamaremos f a la distancia focal, que será positiva para la lente convergente y negativa para la divergente, y d a la distancia entre las dos lentes. Además, como la Luna es un objeto muy distante podemos suponer que se encuentra en el infinito. Vamos a suponer que la primera lente es la convergente (L_C) y la segunda la divergente (L_D). El objeto O está en el infinito, la lente convergente da de él una imagen intermedia O´ y la divergente da la imagen final O´´ que por ser real estará situada a la derecha de dicha lente. Actúa por tanto en primer lugar la lente convergente, para la cual:

Como la distancia imagen es positiva la imagen O´ se forma a la derecha de la lente convergente. A continuación actúa la lente divergente, para la cual el objeto es O´ y la imagen es O´´. Por ser divergente, el objeto y la imagen están al mismo lado de la lente. Sabemos que la imagen está a la derecha de la lente, ya que es real, luego el objeto también estará a la derecha de la lente, y tendremos lo que aparece en la figura.

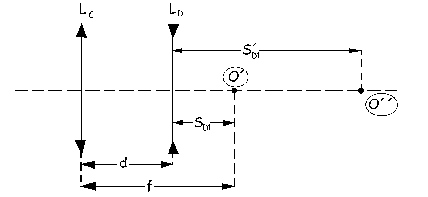
Para la lente divergente:

Ahora se invierten las lentes, y se colocan a la misma distancia d pero primero la divergente y después la convergente. Actuará en primer lugar la lente divergente para la cual:

Como la distancia imagen es negativa, la imagen intermedia O´ se forma a la izquierda de la lente divergente. Actuará ahora la lente convergente.

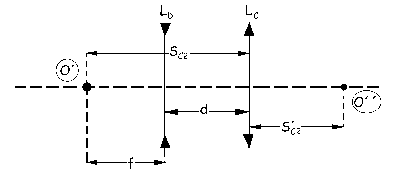
Teniendo en cuenta que la imagen final es real y que por tanto está a la derecha de la lente convergente tendremos:

Nos dicen que en estos dos casos la imagen se desplaza 20 cm luego:

2fd=20d ⇒ 2f=20 ⇒ f=10 cm

f=10 cm

Puede comprobarse que si se supone en primer lugar que primero se coloca la lente divergente y después se invierten el resultado es exactamente el mismo.