Problema de Óptica geométrica

Una lente biconvexa está hecha de vidrio con un índice de refracción de 1.5 respecto al aire que la rodea. Los valores de los radios de curvatura de sus caras son r1=0.3 m y r2=0.2 m. a) Hallar la distancia focal y la potencia; b) determinar la posición y el carácter de un objeto de 3 cm de altura situado sobre el eje 0.5 m a la izquierda de la lente. Repetir las partes a) y b) para una lente convergente cóncavo-convexa del mismo vidrio teniendo los radios de curvatura el mismo valor.

Para la lente biconvexa:
a) f´=0.24 m; P=4.167 dioptrías
b) s´=0.462 m; real invertida y menor
Para la lente cóncavo-convexa:
a) f´=1.2 m; P=0.833 dioptrías
b) s´=-0.857 m; virtual derecha y mayor

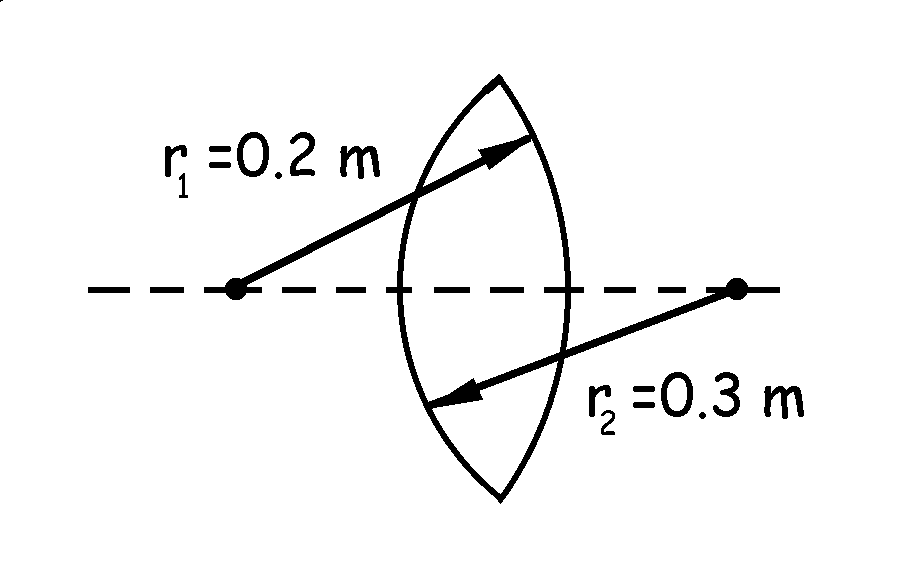a) Para la potencia tendríamos, teniendo en cuenta que la lente es la de la figura:

P=4.167 dioptrías

Y como la focal es el inverso de la potencia:

f´=0.24 m

Podemos ver que habríamos obtenido exactamente lo mismo si hubiéramos colocado la lente al revés, en cuyo caso tendríamos una potencia:

b) Ahora tenemos un objeto situado a la izquierda de la lente y a 0.5 m de ella. La distancia objeto será negativa luego aplicando la ecuación de las lentes delgadas:

S´=0.462 m

Esta imagen será real, ya que estará situada a la derecha de la lente (distancia imagen positiva).

El aumento lateral en este caso será:

El aumento lateral es negativo, luego la imagen es invertida respecto del objeto. Además, como en módulo dicho aumento es menor que la unidad, la imagen será menor que el objeto.

IMAGEN REAL, INVERTIDA Y MENOR

 

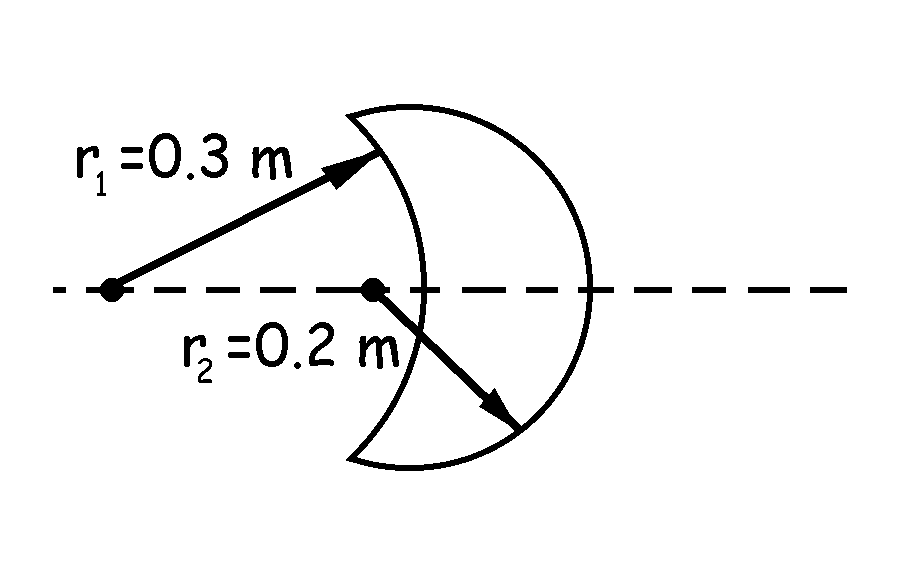Repetimos ahora los dos apartados suponiendo que la lente es cóncavo-convexa.

a) En este caso la potencia de la lente será:

P=0.833 dioptrías

Y la distancia focal:

f´=1.2 m

 

b) Para el objeto situado a 0.5 m de la lente:

S´=-0.857 m

La imagen será virtual, ya que se forma a la izquierda de la lente. En cuanto al aumento lateral:

El aumento lateral es positivo, luego la imagen está derecha respecto del objeto. Además, como en módulo el aumento lateral es mayor que la unidad, la imagen es mayor que el objeto.

IMAGEN VIRTUAL, DERECHA Y MAYOR