Problema de Óptica geométrica

Sean dos lentes convergentes L1 y L2 cuyas distancias focales son 20 cm y 5 cm respectivamente. La L1 está formada por dos lentes delgadas yuxtapuestas, la primera de ellas biconvexa con índice de refracción 1.66 y radios iguales y la segunda bicóncava con índice de refracción 1.52 y radios iguales a la anterior. L1 pueden moverse una respecto de la otra y entre ambas se puede desplazar una tercera lente L3 también convergente de distancia focal 10 cm. Si la posición se elige para que la imagen intermedia dada por L1 de un objeto situado a 1 m de ella se forme delante de L3 a una distancia doble de su distancia focal determinar: a) radios de las lentes que forman el sistema L1 y potencia de la biconvexa y de la bicóncava; b) las posiciones de L1 y L2 para que un ojo situado en el foco imagen de L2 y mirando hacia la izquierda vea a una distancia de 25 cm la imagen del objeto; c) obtener el aumento lateral.

a) r=5.6 cm; Pbiconvexa=23.57 dioptrías; Pbicóncava=-18.57 dioptrías
b) d1=45 cm; d2=24 cm
c) β=1.25

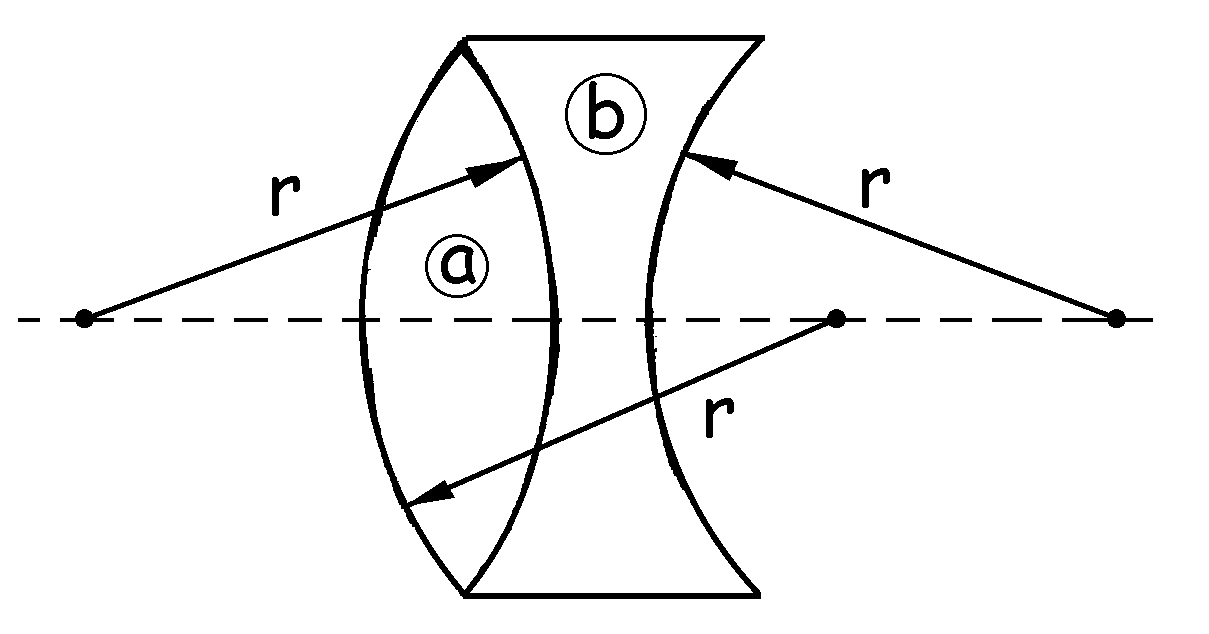a) La lente L1 está formada por las lentes a y b dibujadas en la figura. Denominaremos r al radio común de estas dos lentes. Para la lente a tendremos:

Y para la lente b:

Como las lentes son yuxtapuestas sus potencias son aditivas luego:

r=5.6 cm

Para las potencias de la biconvexa y de la bicóncava no hay más que sustituir. Para la biconvexa:

Pa=23.57 dioptrías

Y para la bicóncava:

Pb=-18.57 dioptrías

b) Las lentes están colocadas en el orden L1 – L3 – L2. Sabemos que el objeto está situado 1 m (100 cm) a la izquierda de L1. La imagen dada por L1 se forma delante de L3 a una distancia doble de su focal, es decir, a una distancia de:

d=2f´3=2 · 10=20 cm

También sabemos que la imagen final, O´´´, es vista a 25 cm por un ojo situado en el foco imagen de L2. Teniendo en cuenta que la distancia focal de L2 es de 5 cm, dicha imagen estará delante de L2 y a 20 cm de ella. Podemos hacer por tanto la representación que aparece en la figura.

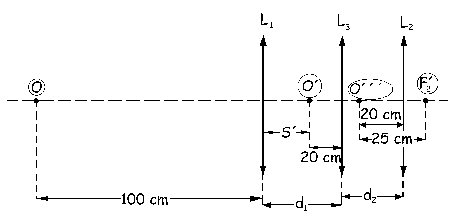
En primer lugar actúa la lente L1, para la cual el objeto es O y la imagen O´. Para esta lente:

Podemos ver en el gráfico adjunto que ya queda determinada una de las distancias:

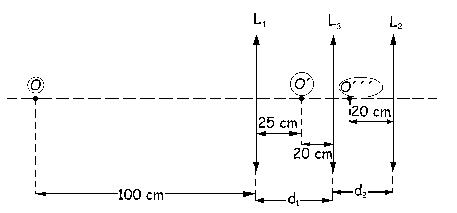
d1=25+20=45 cm

d1=45 cm

A continuación actúa la lente L3, para la cual el objeto es O´ y la imagen será O´´, todavía sin determinar. Para esta lente tendremos:

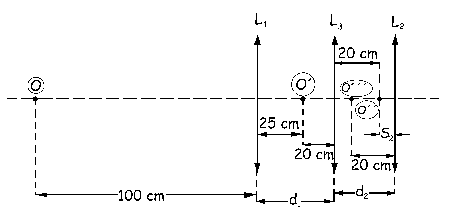
La imagen O´´ se forma a la derecha de L3 y a 20 cm de ella. Como no conocemos d2 podría aparecer la duda de si O´´ está a la derecha o a la izquierda de L2. Para L2 el objeto será O´´ y la imagen O´´´. Vamos a suponer que O´´ está a la izquierda de L2, a una distancia inferior a su distancia focal, con lo cual la imagen sería en efecto virtual. Si esto es cierto, la distancia objeto debería ser negativa y menor de 5 cm, que es la distancia focal. Con esta suposición tendremos:

Vemos que la suposición que hemos hecho es correcta. En el gráfico podemos ver que la distancia d2 es:

d2=20+|S2|=20+4=24 cm

d2=24 cm

 

c) Como tenemos un sistema formado por tres elementos, el aumento lateral será el producto de los aumentos de cada elemento. Como todo el sistema está inmerso en aire (el índice de refracción es la unidad):

β=1.25