.n=1.5
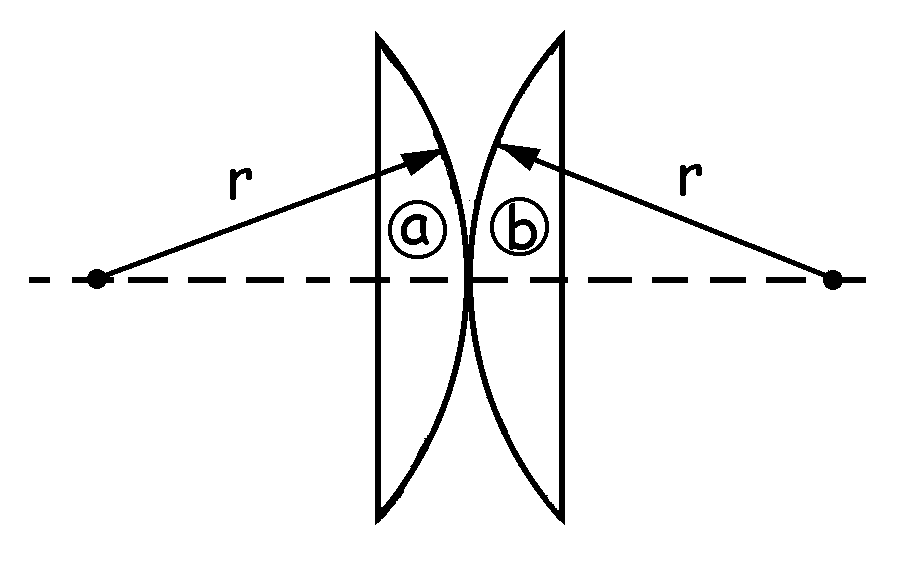En primer lugar tenemos una lente, que llamaremos L1, formada por dos plano-convexas iguales (a y b) en contacto por su cara curva. Esta lente da, para un objeto en el infinito, una imagen real a 164 cm de las lentes; por ser la imagen real, la distancia imagen será positiva. Aplicando a este sistema la ecuación de las lentes delgadas:
A su vez, la lente L1 está formada por dos lentes yuxtapuestas, las lentes a y b. Para lentes yuxtapuestas las potencias son aditivas, luego:
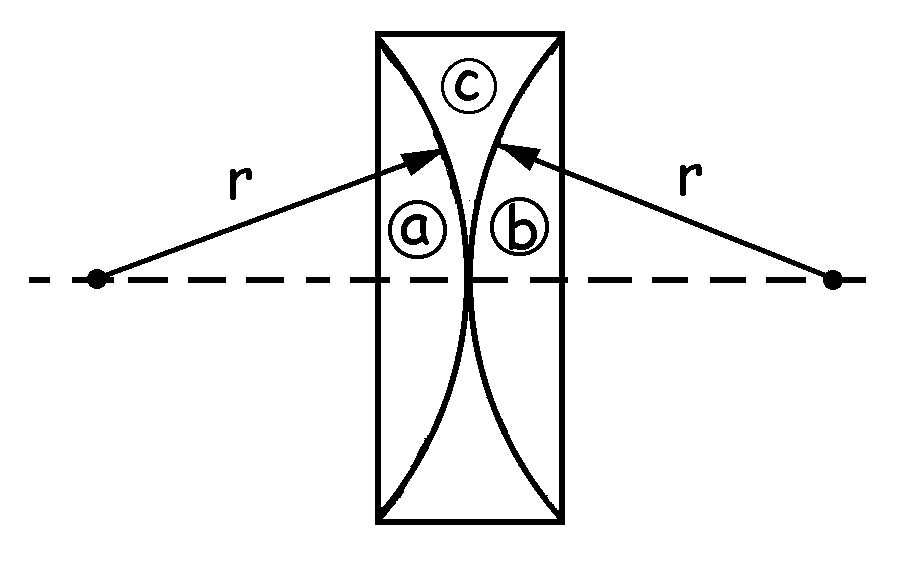A continuación se llena de agua el espacio comprendido entre las dos lentes, con lo cual tenemos otra lente diferente, que llamaremos L2, que si nos fijamos en el gráfico está formada por la yuxtaposición de tres lentes, las dos de antes, más una lente c, bicóncava, que es de agua. Este sistema da una imagen real a 492 cm de las lentes para un objeto en el infinito. Aplicando la ecuación correspondiente:
Esta lente está formada por la yuxtaposición de tres lentes, luego:
P2=Pa+Pb+Pc
Teniendo en cuenta que la yuxtaposición de las lentes a y b forman la lente L1:
P2=Pa+Pb+Pc ⇒ P2=P1+Pc
Sustituyendo esto en la ecuación de la lente L1:
n=1.5