Problema de Óptica geométrica

Aparece en la convocatoria JUN2007

Un sistema óptico está formado por una lente convergente de distancia focal 10 cm y un espejo cóncavo de 3 m de radio. A la izquierda de la lente hay un objeto de 10 cm de longitud que forma un ángulo de 30o con el eje del sistema y cuyo pie dista 20 cm de la lente. La distancia entre la lente y el vértice del espejo es 100 cm. a) Determinar la posición de la imagen final y el ángulo que dicha imagen forma con el eje del sistema óptico; b) se pretende sustituir la lente y el espejo por una única lente convergente que dé una imagen del objeto de tal modo que la distancia entre la proyección del extremo (punto B) y su imagen sea la misma que en el apartado anterior. Calcular la distancia focal y la posición (distancia al objeto) de dicha lente; c) si dicha lente es cóncavo-convexa con un índice de refracción de 1.5 y sus radios de curvatura están en la relación 1 a 3 calcular dichos radios. Todas las lentes pueden considerarse delgadas.

a) s´A´=171.43 cm; α=15.07o
b) f´=12.31 cm; sB=13.79 cm
c) r1=12.31 cm; r2=4.10 cm

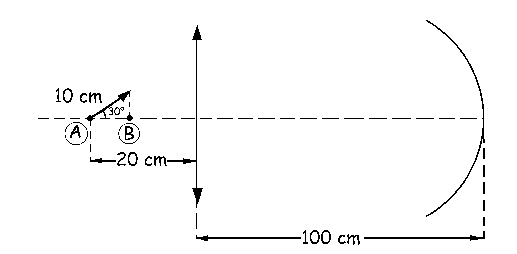
a) Vamos a determinar las imágenes de los puntos A y B para fijar las posiciones de la imagen final. En primer lugar actúa la lente y tendremos que para el punto A:

Y para el punto B:

Podemos dibujar entonces las imágenes intermedias de los puntos A y B (A´ y B´) dadas por la lente.

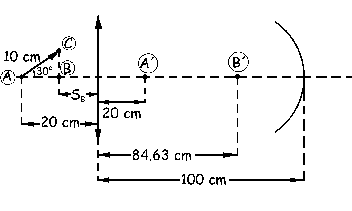
A continuación actúa el espejo (radio de curvatura negativo por ser un espejo convexo), para dar de los puntos A´ y B´ las imágenes finales A´´ y B´´. Para el punto A´:

SA´=-(100-20)=-80 cm

Por tanto al pasar por el espejo:

S´A´=171.43 cm

Y para el punto B´:

SB´=-(100-84.63)=-15.37 cm

Y tendremos un punto imagen a una distancia:

El aumento lateral del sistema será el producto de los aumentos de los elementos que lo forman, luego:

Dado que el aumento lateral es también la relación entre el tamaño de la imagen y el tamaño del objeto, la altura de la imagen final será entonces:

Nos quedaría el gráfico adjunto.

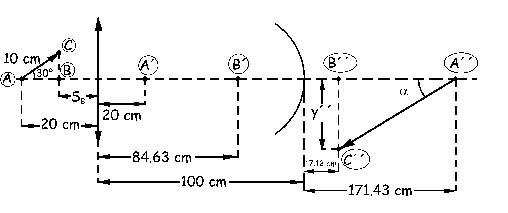
El ángulo α que forma la imagen final con el eje se puede determinar de forma sencilla mediante trigonometría:

α=15.07º

 

b) En el enunciado nos dicen que se debe conservar la distancia entre el punto B y su imagen B´´, que podemos ver en la figura que vale:

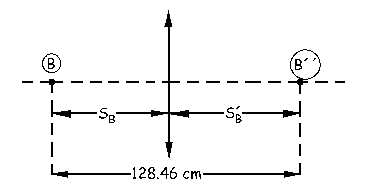
BB´´=11.34+100+17.12=128.46 cm

Tendríamos entonces únicamente una lente convergente, los puntos B y B´´ y que se debería conservar también el aumento lateral.

Si utilizamos únicamente los módulos tendremos las ecuaciones:

SB+S´B=128.46

De la primera ecuación:

Y sustituyendo en la segunda

SB+S´B=128.46 ⇒ SB+8.313SB=128.46
9.313SB=128.46 ⇒ SB=13.79 cm

SB=13.79 cm

La distancia imagen será:

S´B=8.313SB=8.313 · 13.79=114.67 cm

Tenemos sólo los módulos. Ahora habrá que tener en cuenta que la distancia objeto es negativa, mientras que la distancia imagen es positiva. Para una lente delgada:

f´=12.31 cm

 

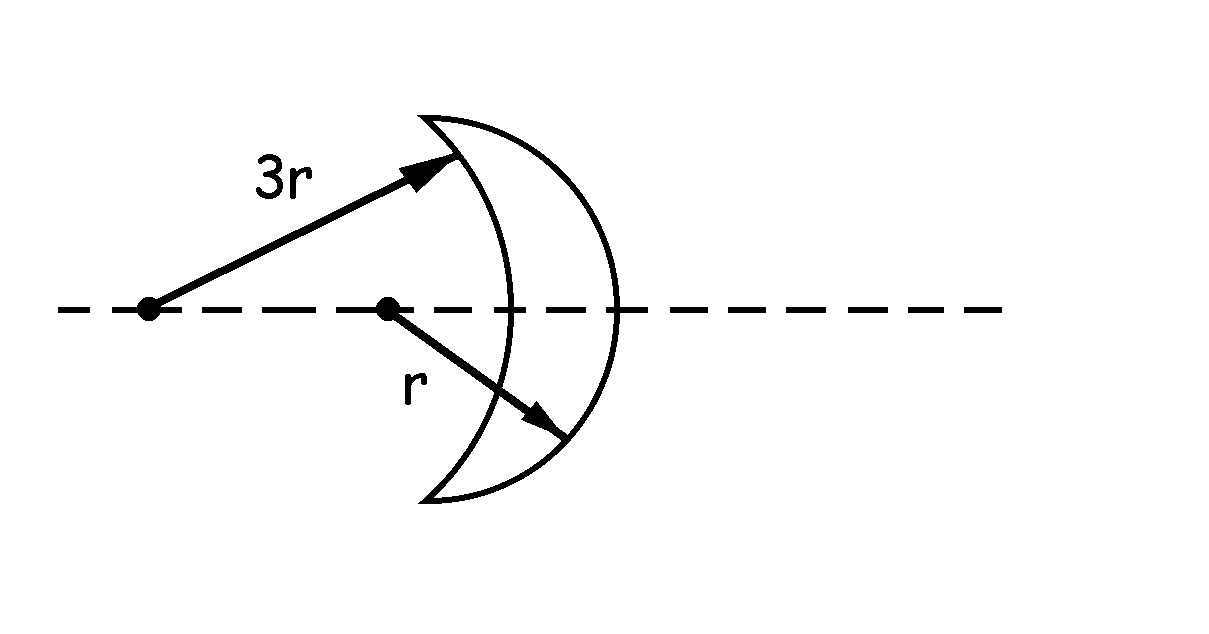c) Por último tendremos una lente cóncavo-convexa, que será tal como aparece en la figura. Ya tenemos en cuenta que los radios están en la relación 1 a 3. Para esta lente:

Entonces el radio de la primera cara es:

r1=3r=3 · 4.10=12.31 cm

r1=12.31 cm

Y el de la segunda:

r2=r=4.10 cm

r2=4.10 cm