a) f´1=25 cm
b) Imagen virtual, invertida y de menor tamaño
c) L1H=6 cm, L2H´=-7.5 cm, f´1=12 cm, f´2=15 cm.
Primera parte
a) Denominaremos a la lente biconvexa lente a y a la cóncavo-convexa lente b. Para la potencia tendríamos:
En el caso de la lente a:
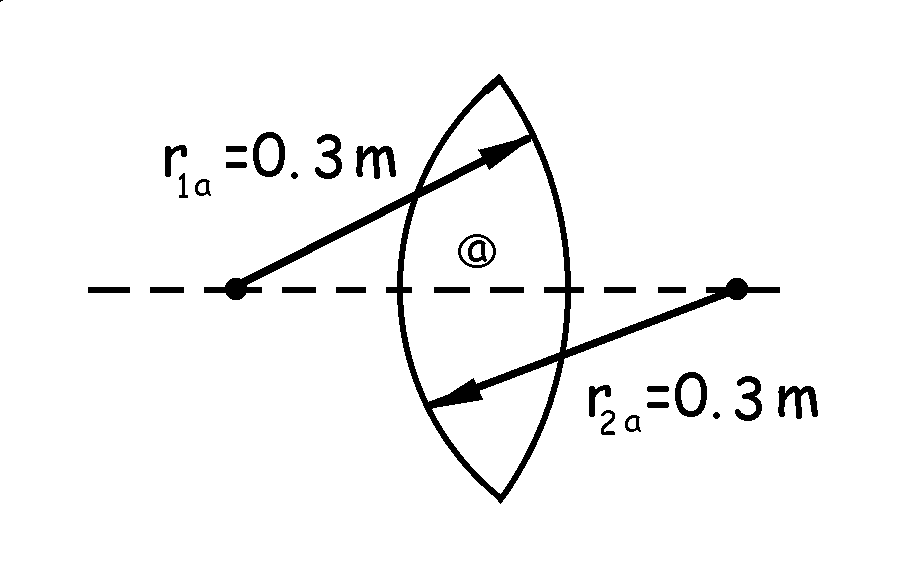
![]()
En el caso de la lente b:
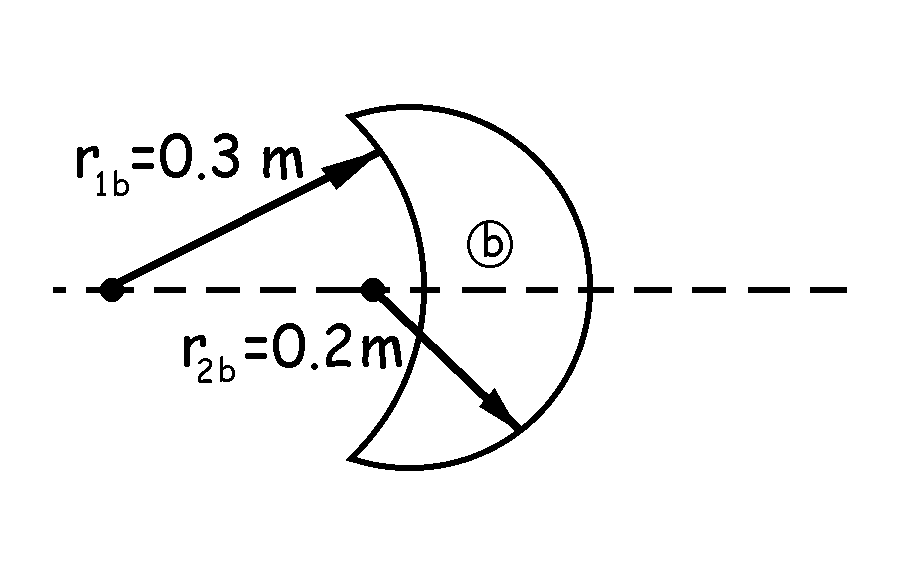
![]()
Como las dos lentes yuxtapuestas que forman la lente 1 son delgadas la potencia es aditiva:
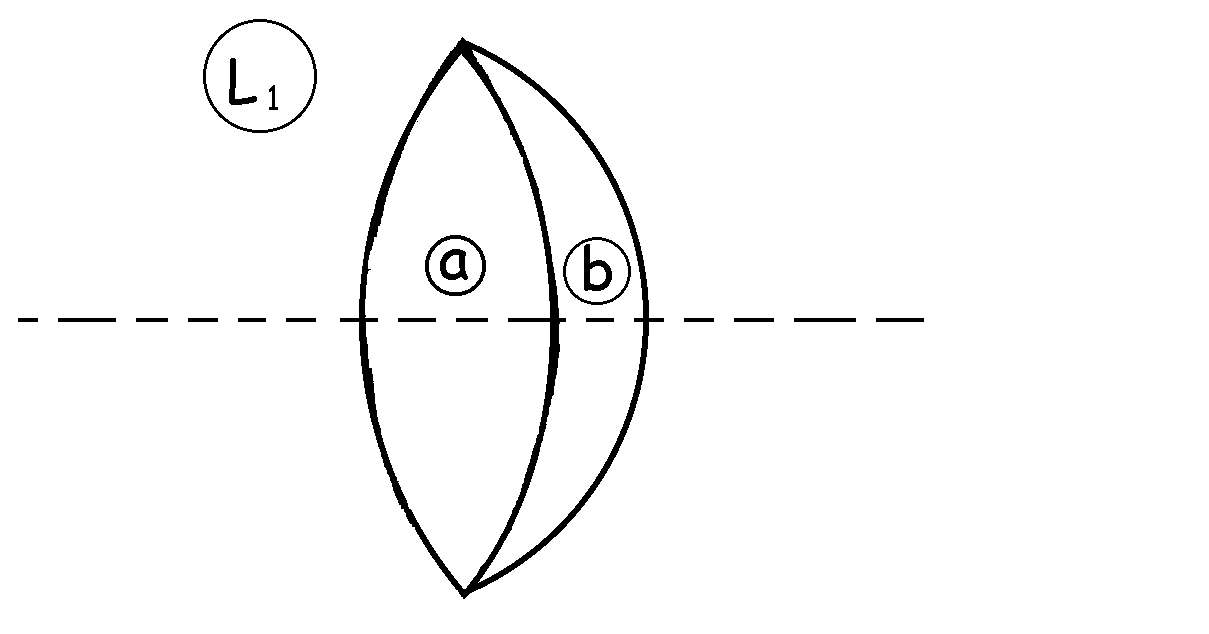
![]()
f´1=25 cm
b)Tenemos el objeto inclinado 30o que representaremos con una flecha, tal como aparece en la figura. Determinaremos en primer lugar la imagen que da la lente L1 del punto P, que es el pie del objeto. Para este punto:
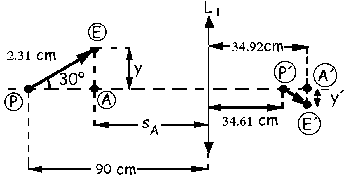
![]()
Ahora vamos a determinar las imágenes de los puntos A y E, para así formar la imagen. Para el punto A tendremos:
![]()
Y para el la imagen del punto E vamos a utilizar el aumento lateral. Dicho aumento vale, teniendo en cuenta que a ambos lados de la lente hay aire:
![]()
A su vez el aumento lateral es la relación entre el tamaño de la imagen y el tamaño del objeto. Por tanto:
![]()
Nos aparece entonces el sistema de la figura. Esa imagen P´E´actua de objeto para la segunda lente L2 cuya focal es 10 cm. Tendremos ahora siguiendo los mismos pasos anteriores:
![]()
![]()
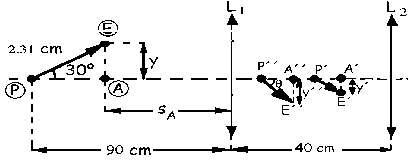
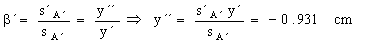
El ángulo θ que forma la imagen con el eje óptico tiene una tangente cuyo valor es: ![]()
Tamaño de la imagen: P´´E´´=![]() cm
cm
La imagen es virtual, invertida y de menor tamaño
Segunda parte:
c) Los puntos donde los planos principales, objeto e imagen cortan al eje ópticos los llamaramos H y H´respectivamente.
Aplicando la ecuación de las lentes podemos calcular la distancia focal imagen del sistema compuesto equivalente:
![]()
Como por otra parte la imagen de la primera lente se forma a 16 cm a la izquierda del plano principal imagen del S.O.C. tenemos, por tanto:
![]()
L1H=6 cm
Para determinar le distancia focal de la lente L2 aplicamos la ecuación:
![]()
f´2=15 cm
Para calcular la distancia focal de la lente L1 utilizamos la ecuación:
![]()
f´1=12 cm
Antes de poder dibujar el sistema óptico vamos a determinar la posición la posición del plano principal imagen respecto a la lente L2
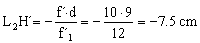
L2H´=-7.5 cm
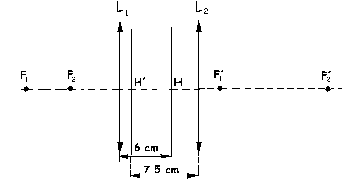
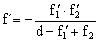 ; distancias de las lentes a los planos principales:
; distancias de las lentes a los planos principales: 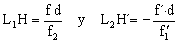 )
)