a) νfund=84.8 s-1
b) v= 339.2 m/s
c) ν=1004 s-1
a) En el primer caso, para el tubo de longitud L = 1m, deduzcamos la ecuación de las ondas (estacionarias):
La ecuación genérica de una onda estacionaria es:
![]()
En este caso de tubo cerrado por un extremo (x=0) y abierto por el otro (x=L) tendremos como condiciones de contorno:
![]()
![]()
que llevan a:
![]()
![]()
Así, obtenemos como condición sobre el vector de ondas k:
![]()
con N perteneciente a los números enteros.
En términos de la frecuencia quedará:
![]()
Obtenemos así la frecuencia en función de la velocidad de las ondas sonoras en el tubo y de la longitud L del mismo. El número N da cuenta de las distintas frecuencias emitidas:
N=0, frecuencia fundamental.
N=1, 1er armónico
N=2, 2º armónico, etc..
Sustituyendo para L = 1m, las frecuencias correspondientes al 2º armónico (N=2) y a la vibración fundamental (N=0) son:
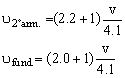
Si dividimos ambas expresiones obtenemos:
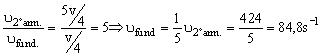
Por lo tanto, tenemos:
![]()
b) La velocidad de las ondas sonoras en el interior del tubo, se puede calcular como:
![]()
Por tanto:
v= 339,2 m/s
c) Consideremos ahora los dos compartimentos diferentes del tubo. En este caso, para cada compartimento tenemos unas condiciones diferentes:
1er compartimento: L1 = 0,75 m, T1 = 88 ºC. Cerrado por ambos extremos.
La ecuación de ondas estacionaria, deducida a partir de la expresión genérica:
![]()
tiene como condiciones de contorno (al estar cerrado por ambos extremos):
![]()
![]()
que llevan ahora a:
![]()
![]()
Así, obtenemos como condición sobre el vector de ondas k1:
![]()
con N1 perteneciente a los enteros.
En términos de la frecuencia queda:
![]()
2º compartimento: L2 = 0,25 m, T2 = 20 ºC. Un extremo cerrado y otro abierto.
Tendremos, como ya se dedujo en a):
![]()
con N2 perteneciente a los enteros.
En términos de la frecuencia quedará:
![]()
Tenemos por tanto expresiones diferentes para la frecuencia en cada uno de los compartimentos, en términos de las longitudes y velocidades del sonido en cada uno de ellos, y de los índices N1 y N2. Sin embargo, la frecuencia en ambos compartimentos debe ser la misma, por lo que:
![]()
de donde se tiene una relación entre los valores de N1 y N2. Los valores más pequeños de ambos índices, compatibles, nos darán la frecuencia más baja para la que se producen ondas estacionarias en ambos compartimentos.
Necesitamos conocer la velocidad del sonido en cada compartimento. Puesto que el 2º compartimento se mantiene a 20 ºC, la velocidad del sonido es la calculada en b), v2=339,2 m/s. Para calcular la velocidad en el primer compartimento, que está a 88 ºC, recordemos la relación entre la velocidad del sonido y la temperatura:
![]()
Así tendremos:
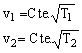
de donde dividiendo ambas expresiones y sustituyendo los valores de las temperaturas se tiene:
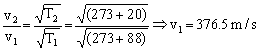
Sustituyendo los valores de v1, v2, L1 y L2 en la ecuación anterior, tendremos:
![]()
Dando valores a N2, obtenemos:
N2=0 ⇒ N1=1,35 (No válido)
N2 =1 ⇒ N1= 3.1,35=4.05 ≈ 4 (válido)
N2 =2 ⇒ N1= 5.1,35 = 6,75 (No válido)
….
Por lo tanto, los números enteros N1 y N2 menores y que llevan a valores iguales de las frecuencia en ambos tubos son: N2 = 1 y N1 = 4
Podemos calcular ya la frecuencia como:
![]()
ν= 1004 s-1