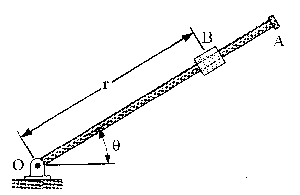
a) v=0; a=120 mm/s2
b) v=170.88 mm/s; a=905.1 mm/s2
c) v=180 mm/s; at=-240 mm/s; an =-4320 mm/s2
a) Los valores de las derivadas de r y θ son:
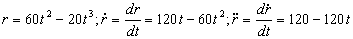
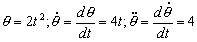
En polares, la velocidad será:
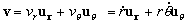
Para t=0:
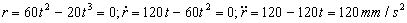
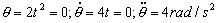
Entonces, sustituyendo:
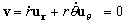
v=0
La aceleración en polares es:
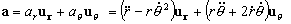
Tendremos que para t=0 obtenemos:

a=120 mm/s2
b) Para t=1 s tendremos:

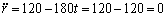
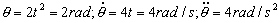
Sustituyendo la velocidad será:
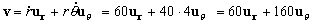
En módulo:
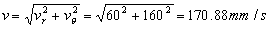
v=170.88 mm/s
Y la aceleración:
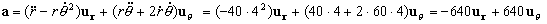
En módulo:
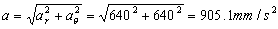
a=905.1 mm/s2
c) El pasador vuelve a pasar por el origen en un tiempo:
r=0 ⇒ 60t2-20t3=0 ⇒ t=3 s
Para t=3 s tendremos:
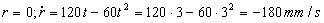
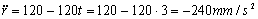
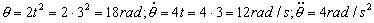
Entonces sustituyendo la velocidad es:
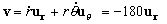
v=180 mm/s
Y la aceleración:
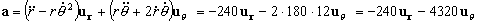
En módulo la velocidad vale:
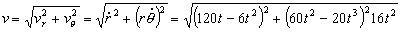
La aceleración tangencial es la derivada del módulo de la velocidad respecto del tiempo, luego valdrá:
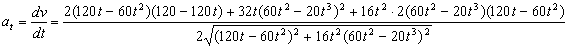
Para t=3 s tendremos:

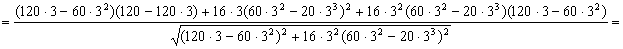
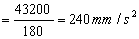
at=240 mm/s2
Y la aceleración normal será:

an=4320 mm/s2
Hay una forma más fácil de determinar las componentes tangencial y normal de la aceleración. En componentes polares la velocidad vale:

Y en intrínsecas:
v=vut
Por tanto un vector unitario en dirección tangencial será:
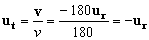
La velocidad por tanto sólo tiene componente en dirección tangencial o radial, ya que dichas direcciones, aunque con sentido contrario, coinciden. En módulo:
v=180 mm/s
La aceleración vale, en coordenadas polares:
a=-240ur-4320uq
Y en intrínsecas:
a=at+an=atut+anun
La aceleración tangencial es la proyección del vector aceleración sobre la dirección tangencial. Para proyectar un vector sobre una dirección dada se multiplica escalarmente el vector por un unitario en la dirección pedida. Tendremos que según esto la aceleración tangencial será:
at=a·ut=(-240ur-4320uθ)·(-ur)=240 mm/s2
at=240 mm/s2
Y en módulo, para la aceleración normal tendríamos, como antes:
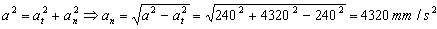
an=4320 mm/s2