a) δ=1.435 oC; β=-0.6447 oC
b) t=9.18 oC
a) Para hallar el valor de la constante δ calcularemos previamente la temperatura del platino del punto de ebullición del azufre, que será (prescindimos de escribir las unidades dentro de la ecuación):
![]()
Así, aplicando la ecuación de Calendar-Van Dusen a este punto, y teniendo en cuenta que como esta temperatura es mayor que cero el parámetro β es nulo tendremos:
![]()
De donde obtenemos ya el parámetro δ:
δ=1.435ºC
Conocido este parámetro la ecuación de Calendar-Van Dusen nos queda:
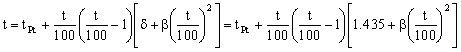
De la misma forma, para determinar el otro parámetro calcularemos primero el valor de la temperatura del platino del punto de ebullición del oxígeno:
![]()
Como esta temperatura ya no es superior a cero, el parámetro β ya no se anula. Nos quedará ahora la ecuación de Calendar-Van Dusen para el oxígeno:

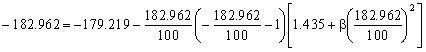
De donde obtenemos el otro parámetro:
β=-0.6447ºC
b) Para calcular la temperatura t asociada con la resistencia de 25.186 Ω lo primero que debemos hacer es calcular la correspondiente al platino:
![]()
Como es superior a cero, no muy superior a cero, el parámetro β no es nulo sino que tiene el valor anteriormente calculado. La ecuación de Calendar-Van Dusen nos queda, teniendo en cuenta que ya hemos determinado los parámetros β y δ:

Si sustituimos la temperatura del platino por el valor obtenido:
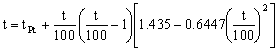

Tenemos una ecuación y una incógnita, la temperatura. Sin embargo, es muy difícil despejar ahí t. Para resolver esta ecuación lo que puede hacerse es ir dando valores a t al azar, e ir viendo cómo el primer miembro y el segundo se aproximan. Cuando ambos se hacen iguales, el valor de t es la solución de la ecuación. Haciendo esto:
Para t=10ºC ⇒ 10≠9.17
Para t=11ºC ⇒ 11≠9.15
Para t=9ºC ⇒ 9≠9.18
Para t=9.5ºC ⇒ 9.5≠9.17
Para t=9.3ºC ⇒ 9.3≠9.178
Para t=9.2ºC ⇒ 9.2≠9.18
Para t=9.18ºC ⇒ 9.18=9.18
Por tanto este es el valor correcto:
t=9.18ºC

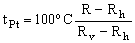 es la denominada temperatura del platino y Rh y Rv son, respectivamente, los valores de R en los puntos de hielo (0 oC) y de vapor de agua (100 oC). Las constantes δ y β son características del platino y están relacionadas con el comportamiento no lineal de la variación de R con t; si δ y β fueran nulas, la variación sería lineal y la temperatura del platino coincidiría con la temperatura Celsius. Considerando un termómetro para el que Rh=24.236 Ω y Rv=34.452 Ω, se pide: a) determinar las constantes δ y β teniendo en cuenta que en los puntos de ebullición normal del azufre (444.674 oC) y del oxígeno (-182.962 oC) la resistencia del termómetro es de 67.417 Ω y 5.927 Ω respectivamente, y que β=0 oC para t>>0 oC; b) calcular la temperatura correspondiente a una resistencia R=25.186 Ω.
es la denominada temperatura del platino y Rh y Rv son, respectivamente, los valores de R en los puntos de hielo (0 oC) y de vapor de agua (100 oC). Las constantes δ y β son características del platino y están relacionadas con el comportamiento no lineal de la variación de R con t; si δ y β fueran nulas, la variación sería lineal y la temperatura del platino coincidiría con la temperatura Celsius. Considerando un termómetro para el que Rh=24.236 Ω y Rv=34.452 Ω, se pide: a) determinar las constantes δ y β teniendo en cuenta que en los puntos de ebullición normal del azufre (444.674 oC) y del oxígeno (-182.962 oC) la resistencia del termómetro es de 67.417 Ω y 5.927 Ω respectivamente, y que β=0 oC para t>>0 oC; b) calcular la temperatura correspondiente a una resistencia R=25.186 Ω.