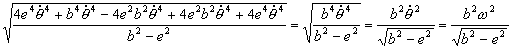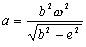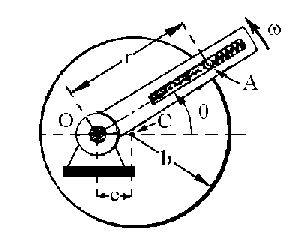
Podemos ver en la figura la nomenclatura que seguiremos con los correspondientes ejes coordenados elegidos. Además, tenemos que la partícula A se mueve con velocidad angular constante, con lo cual podemos deducir:
En coordenadas polares la velocidad vale:
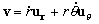
Tendremos que calcular r, θ y sus correspondientes derivadas. Para ello vamos a utilizar la ecuación de la trayectoria. Tenemos una circunferencia cuyo centro está desplazado una cantidad e. La ecuación será entonces:
(x-e)2+y2=b2
En términos de r y θ podemos ver a partir del gráfico que la ecuación quedaría:
(rcosθ-e)2+(rsenθ)2=b2
Para θ=π/2 tendremos:
senθ=1; cosθ=0
Con lo cual:
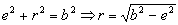
Y ya tendríamos r cuando θ=π/2. Ahora vamos a ir buscando las demás derivadas. Tenemos la ecuación de la trayectoria:
(rcosθ-e)2+(rsenθ)2=b2
Para hallar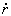 
derivamos esa expresión respecto del tiempo:
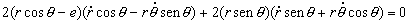
Desarrollando todos los paréntesis:
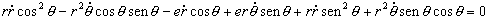
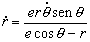
Cuando θ=π/2 nos queda:
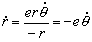
Por lo tanto, la velocidad cuando θ=π/2 será:
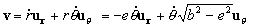
Y en módulo:
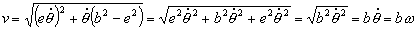
v=bω
Ahora, la aceleración es:
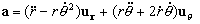
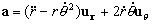
Para hallar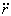 
tenemos la expresión de 
:
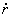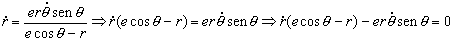
Derivando esta expresión respecto del tiempo:
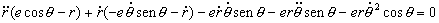
Si tenemos en cuenta que cuando θ=π/2, senθ=1 y cosθ=0, la ecuación se hace más sencilla, quedando:
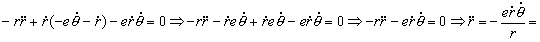
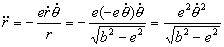
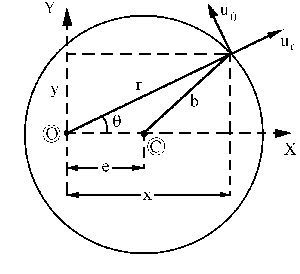
La aceleración entonces vale:
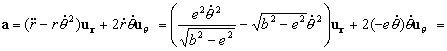
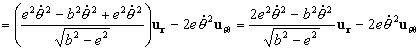
Y en módulo tendremos:
=
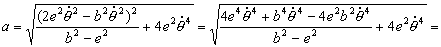
