a) v_c=1680.15 m/s; Φ_c=87.48^o
b) Δv_A=36.50 m/s
c) Δm=22.26 kg
d) Φ_D=88.27^o

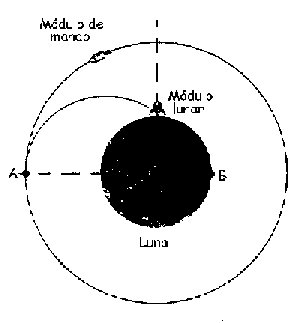
a) Llamaremos órbita 1 a la órbita elíptica que describe el módulo lunar desde la superficie de la Luna hasta el punto A, y órbita 2 a la órbita circular. El radio de la órbita circular es:

r₂=r_A=h_A+R=80+1740=1820 km

La ecuación de la cónica que describe el móvil para ir desde la superficie de la Luna hasta el punto A será:

Para el punto de la superficie de la Luna donde se encuentra el módulo lunar, que llamaremos punto C, conocemos r y θ:

r=r_C=1740 km; θ=90º ⇒ cosθ=0

Aplicando a este punto la ecuación de la cónica tendremos:

Por tanto la ecuación de la cónica nos queda:

Conocemos también r y θ para el punto A, que serán:

r_A=1820 km; θ=180º ⇒ cosθ=-1

Aplicando la ecuación de la cónica al punto A:

Por tanto la ecuación de esta cónica es:

En el pericentro de esta cónica, punto que llamaremos P, tendremos que:

r=r_P ⇒ θ=0º ⇒ cosθ=1

Con lo cual aplicando la ecuación de la cónica:

El eje mayor de la cónica será:

2a₁=r_A+r_P=1820+1666.67=3486.67 km

En esta órbita la energía se mantiene constante; por tanto, si aplicamos la conservación de la energía al punto C tendremos:

v_C=1680.15 m/s

La velocidad que tendrá el módulo lunar en A será, aplicando también la conservación de la energía:

En esta órbita también se conserva el momento cinético o angular. Si aplicamos esta conservación entre los puntos A y C tendremos:

L_A=L_C ⇒ r_Amv_Asenφ_A=r_Cmv_Csenφ_C ⇒ r_Av_Asenφ_A=r_Cv_Csenφ_C

siendo φ_A y φ_C los ángulos que en cada punto la velocidad forma con el radio vector. En el punto A la velocidad y el radio vector son perpendiculares luego:

φ_A=90º ⇒ senφ_A=1

Con lo cual nos queda:

De donde obtenemos:

φ_C=87.48º

 

b) Conocemos la velocidad del módulo lunar en el punto A antes del acoplamiento, que es la que lleva en la órbita elíptica:

v_A=1604.74 m/s

Para que el acoplamiento se produzca de modo adecuado, el módulo lunar debe acelerar para obtener la velocidad del módulo de mando en la órbita circular. En dicha órbita la única fuerza que hay es la de atracción gravitatoria y la única aceleración es la normal o centrípeta. En dicha órbita se cumple por tanto:

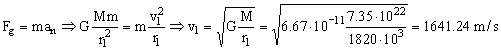
Entonces la variación de velocidad es:

Δv_A=v₁-v_A=1641.24-1604.74=36.50 m/s

Δv_A=36.50 m/s

 

c) Ahora tenemos el sistema total de masa 12000 kg (que representaremos como m_T), que debe pasar de la órbita circular a la órbita elíptica de alunizaje, que llamaremos órbita 3. En la órbita circular la velocidad en el punto A es:

v₁=1641.24 m/s

En la nueva órbita elíptica, si llamamos punto E al punto de alunizaje, cuyo radio coincide con el de la Luna, el eje mayor será:

2a₃=r_A+r_E=1820+1740=3560 km

Aplicamos la conservación de la energía en esta nueva órbita, denominando v_A3 a la velocidad del sistema en el punto A en esta órbita elíptica:

Para los gases que salen de la tobera tendremos:

Δm=22.26 kg

 

d) Cuando la nave tiene una velocidad de 1662 m/s estará en un punto que llamaremos D, en el cual tendrá una velocidad v_D. Aplicando la conservación de la energía a este punto D:

r_D=1777399.7 m=1777.40 km

Y ahora, por conservación del momento angular entre los puntos A y D de la cónica tendremos:

L_A=L_D ⇒ r_Am_Tv_A3senφ_A=r_Dm_Tv_Dsenφ_D ⇒ r_Av_A3senφ_A=r_Dv_Dsenφ_D

siendo φ_A y φ_D los ángulos que en cada punto la velocidad forma con el radio vector. En el punto A, como ya dijimos antes, el velocidad y el radio vector son perpendiculares, luego tendremos:

φ_A=90º ⇒ senφ_A=1

Con lo cual nos queda:

De donde obtenemos:

φ_D=88.27º