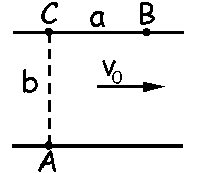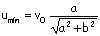
Tomaremos como sistema de ejes el eje X en la dirección AB y el eje Y perpendicular a él. Para llegar al punto B la velocidad absoluta del bote debe tener la dirección AB; además deberá cumplirse que:
u=v–v0
siendo u la velocidad del bote respecto del agua, v la velocidad absoluta del bote y v0 la velocidad absoluta del río. En la figura podemos ver las direcciones de las velocidades v y v0 que son conocidas. No conocemos la dirección de u luego supondremos que forma un ángulo β con la dirección X. Vectorialmente tendremos que la expresión de la velocidad relativa nos queda:
u=v–v0 ⇒ ucosβi+usenβj=vi-v0cosαi+v0senαj
Si separamos componentes en ambos ejes tendremos que para el eje Y debe cumplirse:
En dicha expresión v0 y α son constantes, luego para que u sea mínimo debe ser máximo senβ. El máximo valor de este seno es la unidad luego:
senβ=1 ⇒ β=90º
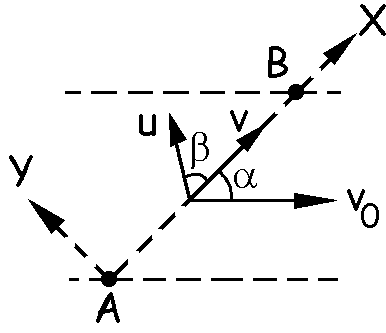
La velocidad relativa será mínima cuando sea perpendicular a la dirección AB (es decir, a v). En este caso nos queda:
