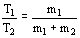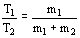
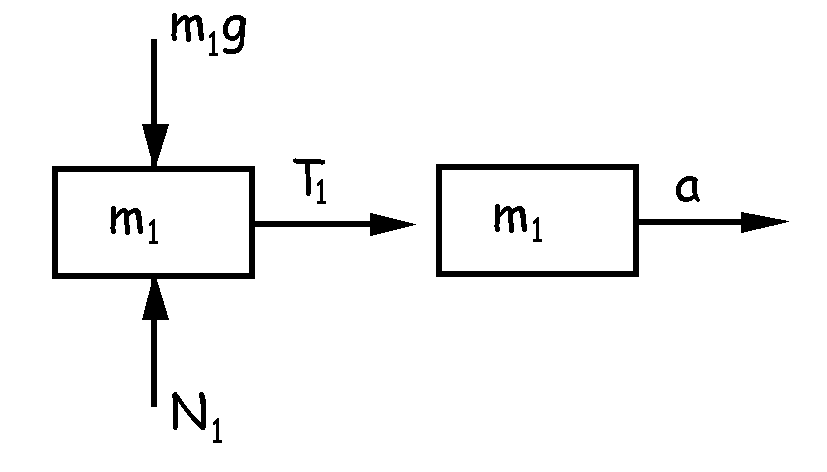
Tomaremos como ejes el eje X horizontal y positivo hacia la derecha, y el eje Y vertical y positivo hacia arriba. Hacemos el diagrama de sólido libre de la masa m1. Sobre ella actúan, vertical y hacia abajo el peso, vertical y hacia arriba la normal, y la tensión T₁ de la cuerda. Como se mueve sólo en la dirección horizontal, la aceleración será a, horizontal y hacia la derecha. Aplicando a este cuerpo la segunda ley de Newton:

ΣF_x=m₁a_1x ⇒ T₁=m₁a

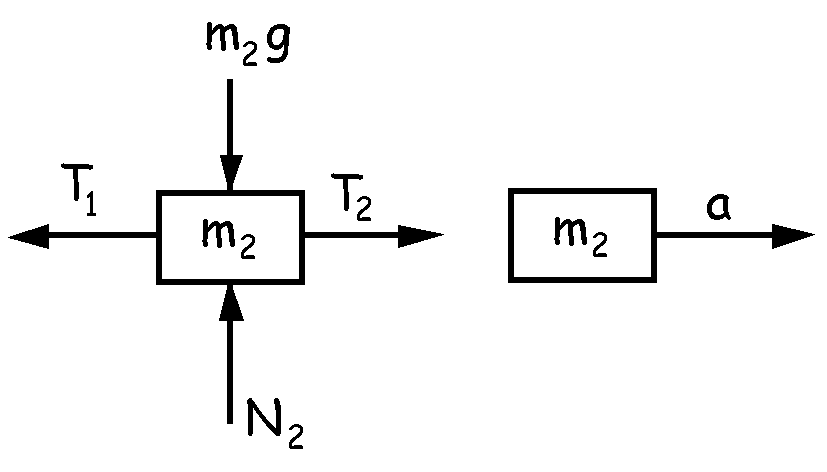Ahora hacemos lo mismo para el cuerpo m₂. En este caso tendremos como antes, que verticalmente actúan la normal y el peso, de sentido contrario que se anularían. Y horizontalmente tendremos las acciones de las dos cuerdas (tensiones). En cuando a aceleraciones, como los dos cuerpos están unidos por la cuerda se mueven a la vez, de modo que ambos están sometidos a la misma aceleración a. Aplicando a este otro cuerpo la segunda ley de Newton:

ΣF_x=m₂a_2x ⇒ T₂-T₁=m₂a

Sustituyendo en esta expresión el valor de T₁ que hemos obtenido en la ecuación del cuerpo m₁:

T₂-T₁=m₂a ⇒ T₂-m₁a=m₂a ⇒ T₂=m₂a+m₁a=(m₁+m₂)a

Dividiendo las expresiones de T₁ y T₂:

De donde obtenemos, simplificando la a: