ν_o=84 Hz; T=635.04 N

Llamaremos T a la tensión que soporta la cuerda y µ a su densidad lineal. La velocidad de una onda en una cuerda tensa viene dada por la expresión:

Para que la cuerda esté recorrida por ondas estacionarias debe verificarse que su longitud sea igual a un número entero de semilongitudes de onda:

Si lo ponemos en función de la velocidad de propagación:

Como los datos que nos dan son de dos armónicos consecutivos, serán de orden n y n+1:

Si sustituimos los datos conocidos:

Dividiendo ambas expresiones:

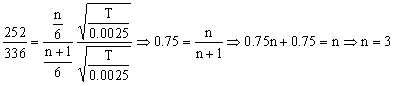
Y el siguiente armónico, de orden n+1 será el de orden 4. La tensión valdrá, despejando:

T=635.04 N

Y el sonido fundamental será:

ν₀=84 Hz