at=9.8 m/s2; an=36 m/s2; a=37.31 m/s2 formando con la horizontal un ángulo de 195.23o

El péndulo realiza un movimiento circular cuyo radio de curvatura es de 1 m. Por trazar una trayectoria curvilínea, su aceleración tendrá dos componentes, la normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura y la tangencial, perpendicular a la normal. En el gráfico vemos las dos componentes de la aceleración en el instante que pide el problema, así como las fuerzas que en ese momento actúan sobre el péndulo. El punto C representa el centro de curvatura mientras que el punto P representa el punto en que está la lenteja del péndulo en ese instante.
Aplicando la segunda ley de Newton a la dirección tangencial tendremos:
Ft=mat ⇒ mg=mat ⇒ at=g=9.8 m/s2
at=9.8 m/s2
La aceleración normal es el módulo de la velocidad al cuadrado partido por el radio de curvatura:
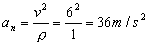
an=36 m/s2
Si representamos ahora este vector tendremos lo que aparece en la figura, donde θ
es el ángulo que forma la aceleración con la dirección positiva del eje X. Podemos calcular α
a través de la tangente:
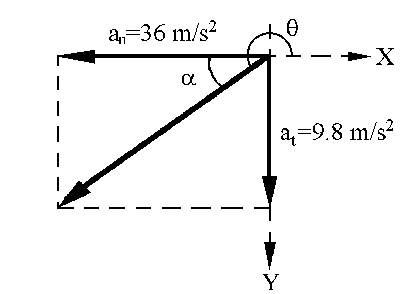
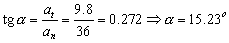
Y el ángulo θ:
θ=180º+α=180º+15.23º=195.23o
θ=195.23º