a) f_A=0; f_A=-4πGm; f_C=-8πGm
b) f_A=0; 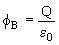; f_C=0

a) Para resolver el problema debemos acudir al teorema de Gauss. Según este teorema, el flujo que atraviesa una superficie cerrada es nulo si la masa es externa a la superficie y -4πGm si la masa m es interna a la superficie. En el caso A las dos masas son externas a la superficie, luego ninguna contribuye al flujo:

f_A=0

En el caso B una masa es interna y la otra externa a la superficie, luego sólo la interna contribuye al flujo:

f_B=-4πGm

Y por último en el caso C las dos masa son internas a la superficie luego ambas contribuyen al flujo:

f_C=-4πGm-4πGm=-8πGm

f_C=-8πGm

 

b) Para el campo eléctrico la ley de Gauss establece que el flujo neto a través de cualquier superficie cerrada está dado por donde Q_int representa la carga neta encerrada en la superficie gaussiana. Por tanto, en el caso A el flujo será nulo porque la superficie gaussiana no encierra carga neta:

f_A=0

En el caso B tendremos:

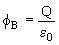
Y en el caso C tendremos:

f_C=0