vX=-9.52 cm/s; vY=7.30 cm/s
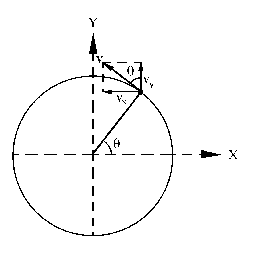
Tenemos que el punto P se mueve en una trayectoria circular. Podemos determinar en qué cuadrante estamos, es decir, determinar el ángulo que forma el radio vector con el origen de coordenadas, ya que el arco es igual al radio por el ángulo. Para t=2 s el arco será:
s=t3+3=23+3=11 cm
Por tanto el ángulo será:
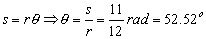
Teniendo en cuenta que el móvil se mueve en sentido antihorario tendremos lo que aparece en el gráfico.
El módulo de la velocidad será además la derivada del espacio respecto del tiempo:
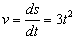
Para t=2 s:
v=3t2=3·22=12 m/s
Y por tanto podemos ver en el gráfico que las proyecciones de la velocidad en los ejes X y Y son:
vx=-vsenθ=-12sen52.52º=-9.52 cm/s
vx=-9.52 cm/s
vy=vcosθ
=12cos52.52º=7.30 cm/s
vy=7.30 cm/s