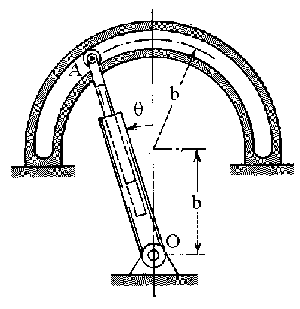
a=4k2b
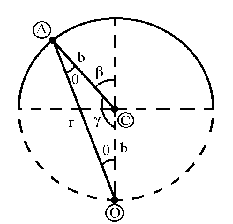
La trayectoria seguida por el punto A es una circunferencia de radio b cuyo esquema aparece en el dibujo. Llamamos O al punto inferior de la circunferencia y C al centro de la misma. El triángulo OCA es un triángulo isósceles, ya que dos de sus lados tienen la misma longitud b, que es el radio de la circunferencia. Por ello, los ángulos opuestos a estos lados son iguales y valen θ. Como los ángulos internos de un triángulo valen 180º tendremos:
2θ+ϒ=180º
Además, puede verse en la figura que:
ϒ+β=180º
De estas dos expresiones podemos deducir que:
β=2θ
Si derivamos esa expresión respecto del tiempo:
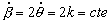
Y volviendo a derivar respecto del tiempo, como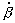 
es constante, tendremos:
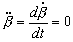
Ahora expresamos la aceleración del punto A en componentes intrínsecas:
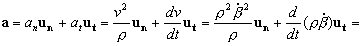
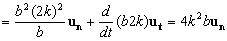
a=4k2b