Problema de Teoría Cinética de los Gases

El volumen cilíndrico de la figura, de sección constante S=1 m2, consta de dos cámaras A y B separadas entre sí por un pistón que a su vez va unido mediante un resorte lineal de constante elástica k=3 N/m a otro pistón provisto de un vástago. El compartimento A contiene helio y el B nitrógeno molecular. La superficie lateral del cilindro es impermeable al calor, lo mismo que los pistones, pero en cambio la base del rectángulo que limita el compartimento B es perfectamente permeable al calor. Inicialmente los dos compartimentos tienen el mismo volumen Vo=2 m3 y la misma presión Po=105 N/m2, siendo su temperatura inicial también la misma e igual a la temperatura constante de la atmósfera exterior. Muy lentamente se va desplazando el vástago hacia la derecha hasta llegar a un estado final en el que la presión en el compartimento A duplica su valor inicial. Sabiendo que los dos pistones se pueden mover sin ningún rozamiento a lo largo del cilindro y que el resorte está inicialmente descargado, se desea calcular el trabajo mecánico que es preciso realizar para hacer esa transformación.

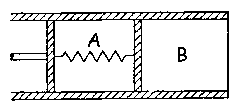
W=-234628.75 J

Llamaremos VA al volumen final del compartimento A y PA a la presión final de este compartimento. La presión nos dice el enunciado que se duplica, luego:

PA=2P0=2 · 105 N/m2

En este compartimento el proceso se realiza sin intercambio de calor, luego tenemos una transformación adiabática. Se cumplirá:

Además, como el helio es un gas monoatómico se cumple que:

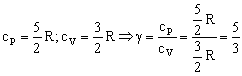
Y sustituyendo en la ecuación de la transformación adiabática:

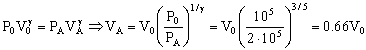
El trabajo necesario para comprimir entonces el helio será el necesario para realizar una compresión adiabática:

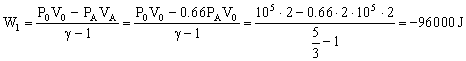
El signo negativo implica que este trabajo es realizado sobre el sistema.

El compartimento B, en el que está el nitrógeno, es permeable al calor, luego siempre se mantiene a la misma temperatura que el exterior. La transformación en este caso será isoterma, luego si llamamos PB y VB a la presión final y al volumen final se deberá cumplir:

PV=cte ⇒ P0V0=PBVB

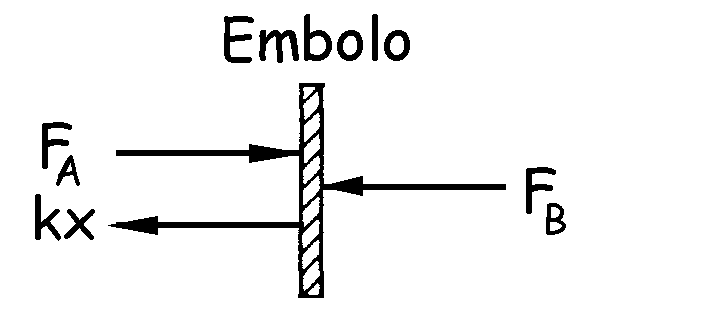El émbolo que separa los dos compartimentos está en equilibrio. Vemos en el gráfico adjunto su diagrama de sólido libre. El gas de la derecha ejerce sobre el émbolo una fuerza que denominaremos FB debida a la presión de este gas (la fuerza será el producto de la presión por la superficie). El gas de la izquierda ejerce sobre el émbolo otra fuerza análoga. Además aparece la fuerza del resorte, que como inicialmente está descargado y sabiendo que el émbolo se mueve hacia la derecha, debe estar estirado. Obviamos las fuerzas verticales ya que sólo analizaremos el eje horizontal. Si llamamos eje X al eje horizontal se verificará entonces que:

ΣFx=0 ⇒ FA-kx-FB=0 ⇒ PAS-kx-PBS=0 ⇒ 2P0S-kx-PBS=0

Podemos determinar x teniendo en cuenta que el volumen será igual a la superficie S dividido por la longitud. Restando el volumen final menos el inicial, y dividiendo por la superficie, tendremos la variación de longitud del resorte:

Y de esta forma podemos determinar la presión final en el compartimento B:

Ahora teníamos que en el gas B se producía una transformación isoterma por lo que se verifica:

P0V0=PBVB

Y el trabajo necesario para realizar la compresión isoterma será:

El término nRT lo podemos determinar a través de la ecuación de los gases perfectos:

PV=nRT ⇒ nRT=PV=P0V0=105·2=2·105 Nm3/m2=2·105 Nm

Sustituyendo:

Por último, habrá que tener en cuenta la energía potencial elástica almacenada en el resorte, que valdrá:

El trabajo mecánico necesario para la transformación será entonces:

W=W1+W2+EPe=-96000-138629.44+0.6936=-234628.75 J

W=-234628.75 J