a) t=2 s
b) v=3.14 m/s
c) Vertical y hacia abajo
d) 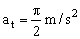 ; an=9.87 m/s2
; an=9.87 m/s2
e) a=9.99 m/s2; θ=9.04o
 a) Tenemos el sistema de la figura. La aceleración tangencial vale:
a) Tenemos el sistema de la figura. La aceleración tangencial vale:
![]()
Por tanto la aceleración angular será:
![]()
Como la aceleración angular es constante, el movimiento es uniformemente acelerado y tendremos:
![]()
De donde obtenemos:
t=2 s
b) En ese momento:
![]()
Y como el movimiento es circular la velocidad lineal será:
v=ω
R=π· 1=π=3.14 m/s
v=3.14 m/s
c) La velocidad es tangente a la trayectoria y tiene el sentido de avance del móvil, luego será vertical y hacia abajo.
VERTICAL Y HACIA ABAJO
d) La aceleración tangencial es constante, luego nos vale la inicial:
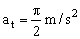
Y la normal:
![]()
an=9.87 m/s2
e) Como estas dos componentes son perpendiculares, el módulo de la aceleración será:
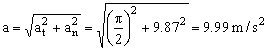
a=9.99 m/s2
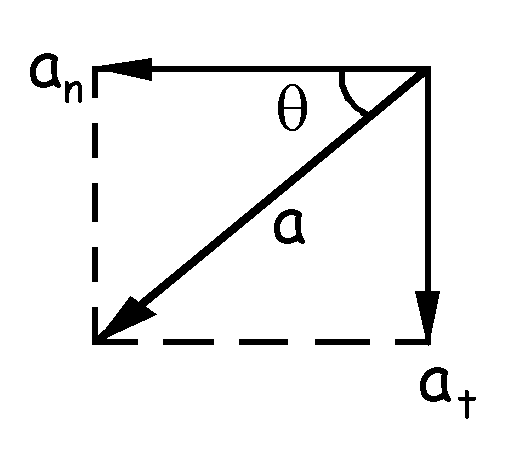 Y para determinar la dirección que tiene esta aceleración no tenemos más que dibujar sus componentes. El ángulo θ valdrá:
Y para determinar la dirección que tiene esta aceleración no tenemos más que dibujar sus componentes. El ángulo θ valdrá:

θ=9.04º