a) θ=60o
b) v=6.26 m/s
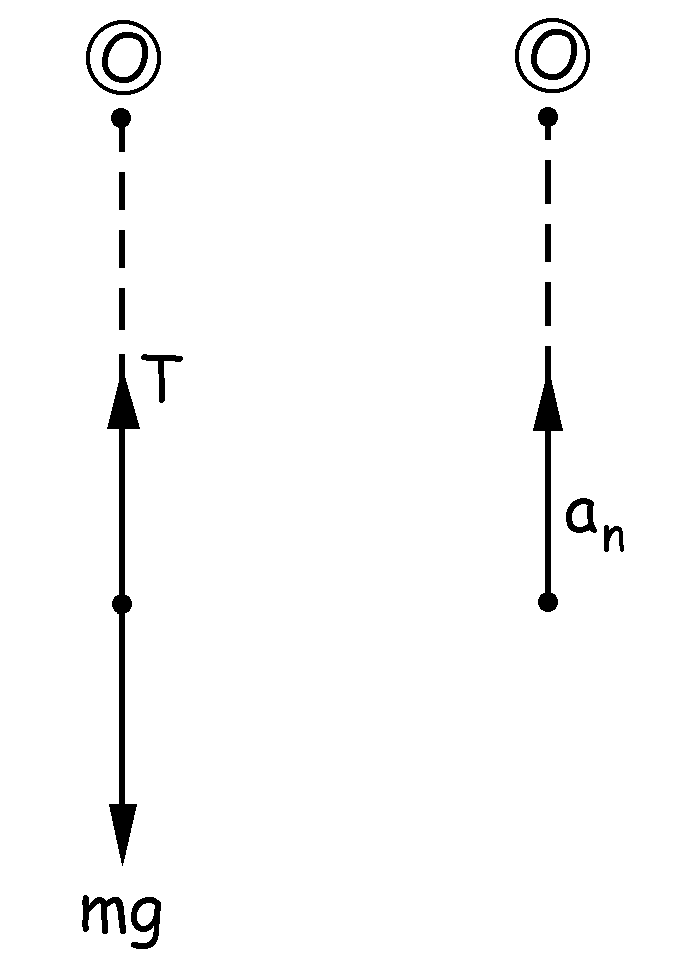 La cuerda se romperá en la posición más baja, ya que ahí la tensión es mayor. Si aislamos al muchacho en ese punto tendremos lo que se muestra en la figura. En cuanto a fuerzas, es muchacho está sometido a su peso y a la tensión de la cuerda. En cuanto a aceleraciones, el movimiento es circular, luego en principio existirán dos aceleraciones, la tangencial y la normal. En este caso, la aceleración tangencial es nula ya que en este punto el módulo de la velocidad es máximo, luego su derivada (aceleración tangencial) es nula. Tendremos sólo aceleración normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura. Aplicando la segunda ley de Newton, llamando m a la masa del muchacho y teniendo en cuenta que la trayectoria es una circunferencia de radio l tendremos:
La cuerda se romperá en la posición más baja, ya que ahí la tensión es mayor. Si aislamos al muchacho en ese punto tendremos lo que se muestra en la figura. En cuanto a fuerzas, es muchacho está sometido a su peso y a la tensión de la cuerda. En cuanto a aceleraciones, el movimiento es circular, luego en principio existirán dos aceleraciones, la tangencial y la normal. En este caso, la aceleración tangencial es nula ya que en este punto el módulo de la velocidad es máximo, luego su derivada (aceleración tangencial) es nula. Tendremos sólo aceleración normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura. Aplicando la segunda ley de Newton, llamando m a la masa del muchacho y teniendo en cuenta que la trayectoria es una circunferencia de radio l tendremos:
![]()
En el momento en que se rompe la tensión que soporta la cuerda es el doble del peso del muchacho:
![]()
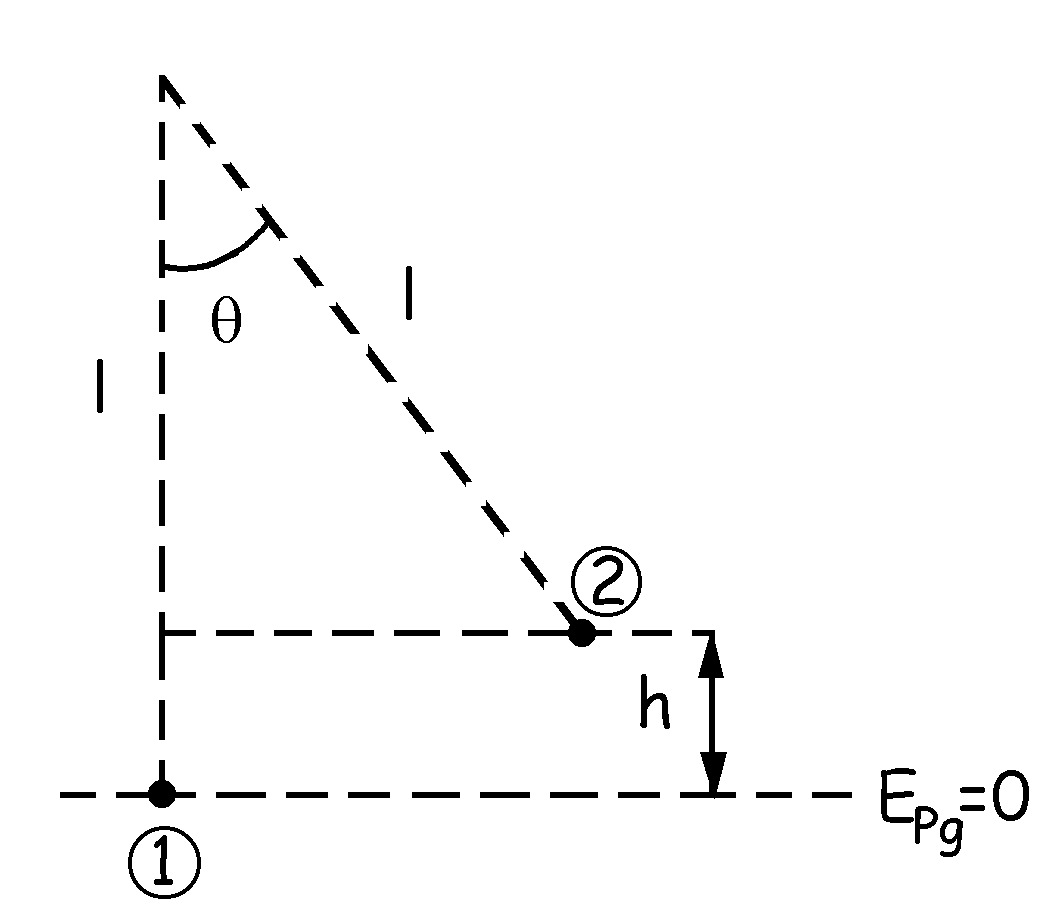 Además tenemos que puesto que no hay fuerzas disipativas la energía mecánica se mantiene constante. Llamaremos situación 1 a la inicial, en que el muchacho se suelta desde el reposo con la cuerda inclinada un ángulo θ respecto de la vertical, y situación 2 al momento en que pasa por la posición más baja. Tomaremos esta posición como nivel de energía potencial gravitatoria nula. Entonces:
Además tenemos que puesto que no hay fuerzas disipativas la energía mecánica se mantiene constante. Llamaremos situación 1 a la inicial, en que el muchacho se suelta desde el reposo con la cuerda inclinada un ángulo θ respecto de la vertical, y situación 2 al momento en que pasa por la posición más baja. Tomaremos esta posición como nivel de energía potencial gravitatoria nula. Entonces:
![]()
![]()
Si ahora tenemos en cuenta el valor que hemos obtenido para la velocidad a partir del sistema de fuerzas:
2gl(1-cosθ)=v2 ⇒ 2gl(1-cosθ)=gl ⇒ 2(1-cosθ)=1
![]()
Con lo cual tenemos:
θ=60º
b) Y la velocidad para este valor será:
v2=gl=9.8 · 4=39.2 m2/s2
v=6.26 m/s
Obtenemos exactamente lo mismo al sustituir en la otra expresión de la velocidad:
v2=2gl(1-cosθ)=2 · 9.8 · 4(1-cos60o)=39.2 m2/s2