a) x= xo-30t; 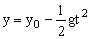
b) x= xo-245t; 
c) θ=+/-28.65o
![]() a) Tenemos que el avión es un sistema de referencia en traslación. La velocidad de 245 m/s es la velocidad de la bala respecto del avión (vB/A), mientras que la de 215 m/s es la velocidad absoluta del avión (vA). Tomaremos como eje X un eje horizontal y positivo hacia la derecha, y como eje Y un eje vertical y positivo hacia arriba. De acuerdo con este sistema:
a) Tenemos que el avión es un sistema de referencia en traslación. La velocidad de 245 m/s es la velocidad de la bala respecto del avión (vB/A), mientras que la de 215 m/s es la velocidad absoluta del avión (vA). Tomaremos como eje X un eje horizontal y positivo hacia la derecha, y como eje Y un eje vertical y positivo hacia arriba. De acuerdo con este sistema:
vB/A=-245i; vA=215i
En el eje X el movimiento es uniforme. La velocidad absoluta de la bala (velocidad respecto de Tierra) será por tanto:
vB/A=vB–vA ⇒ vB=vB/A+vA=-245i+215i=-30i
Luego el espacio recorrido en el eje X:
x=x0+vBxt=x0-30t
x= x0-30t
En el eje Y el movimiento es uniformemente acelerado, ya que la bala está sometida a la aceleración de la gravedad (vertical y hacia abajo). La velocidad inicial en este eje es nula porque la bala se lanza horizontalmente. Entonces el espacio en este eje:
![]()
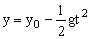
b) Ahora, si tomamos como sistema de referencia el avión, en el eje X tendremos movimiento uniforme, pero la velocidad de la bala deberá medirse respecto del avión:
vB/A=-245i
Por tanto el espacio recorrido es:
x=x0+(vB/A)xt=x0-245t
x= x0-245t
En el eje Y el movimiento sigue siendo uniformemente acelerado, sin velocidad inicial y con aceleración la de la gravedad:
![]()

![]() c) Ahora, si la bala se lanza con un cierto ángulo tendremos lo que aparece en el gráfico. Ahora las velocidades absoluta y relativa del avión y de la bala son:
c) Ahora, si la bala se lanza con un cierto ángulo tendremos lo que aparece en el gráfico. Ahora las velocidades absoluta y relativa del avión y de la bala son:
vA=215i; vB/A=-245cosθi+245senθj
La velocidad absoluta de la bala (respecto de Tierra) será:
vB/A=vB–vA ⇒ vB=vB/A+vA=-245cosθ i+245senθ j+215i=(215-245cosθ)i+245senθj
Si la componente horizontal es nula:
![]()
θ=±28.65º
Puede verse que aparece un doble signo. Nosotros en el gráfico hemos dibujado la solución positiva (la bala se dispara hacia arriba). Es fácil ver que se obtiene exactamente el mismo resultado si suponemos que la bala se dispara hacia abajo (resultado negativo del ángulo).