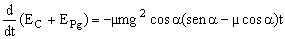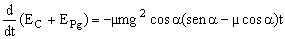
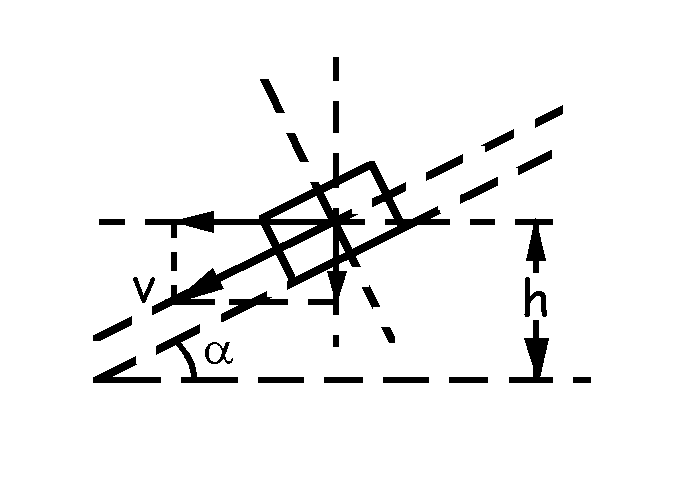
La energía cinética más la potencial en un instante cualquiera serán:

Y su variación en el tiempo:

Tendremos que:

Si aislamos el sistema en un instante cualquiera tendremos lo que aparece en la figura. Aplicando la segunda ley de Newton:

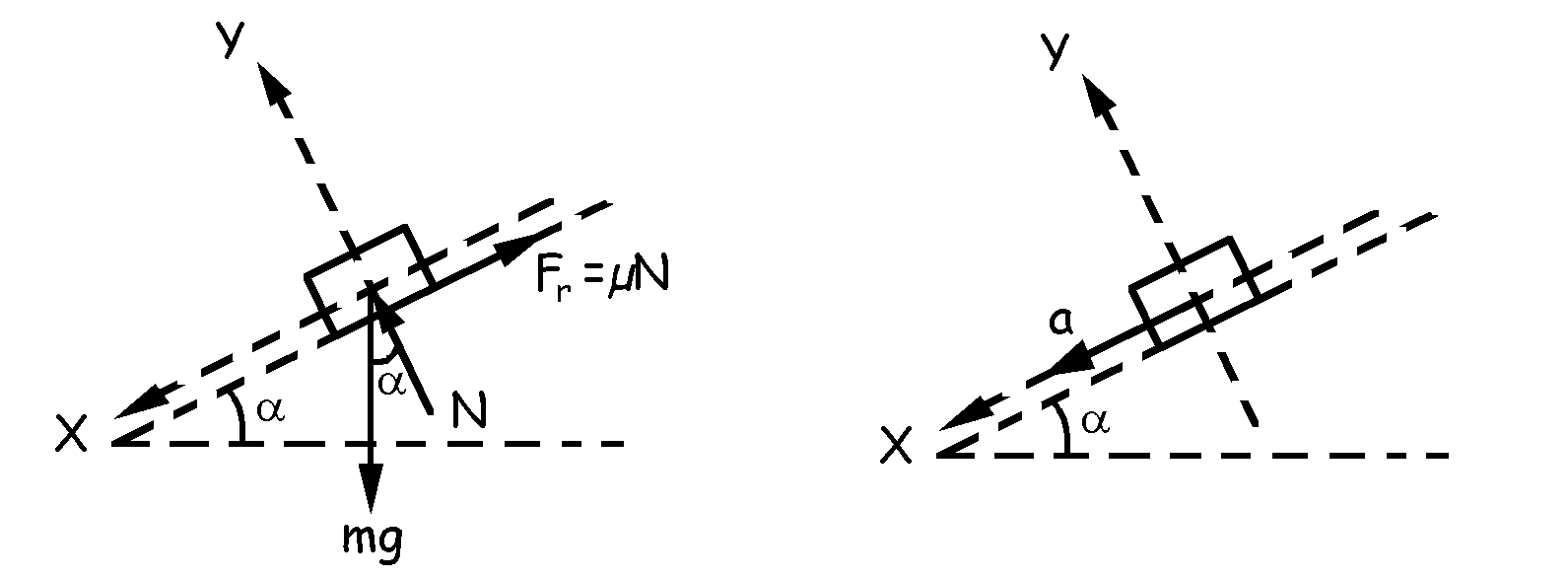
ΣF_y=ma_y ⇒ N-mgcosα=0 ⇒ N=mgcosa

ΣF_x=ma_x ⇒ mgsenα-F_r=ma ⇒ mgsenα-µN=ma ⇒ mgsenα-µmgcosα=ma

a=gsenα-µgcosα=cte

Ya tenemos la derivada de la velocidad respecto del tiempo. Ahora la variación de la altura respecto del tiempo será la componente vertical de la velocidad, con signo negativo puesto que la altura h disminuye a lo largo del tiempo:

Si sustituimos todo en la expresión de la variación de la energía:

=mvgsenα-mvµgcosα-mvgsenα=-mvµgcosα

Como la aceleración es constante, el movimiento es rectilíneo y uniformemente acelerado, luego podemos aplicar las ecuaciones correspondientes de modo que en cualquier instante:

v=v₀+at=at=(gsenα-µgcosα)t

Por tanto:

=-µm(gsenα-µgcosα)tgcosα=-µmg²cosα(senα-µcosα)t

En módulo: