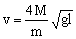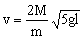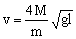
; 
En primer lugar se produce un choque, luego se conserva la cantidad de movimiento. Antes y después del choque sólo tendremos movimiento en el eje X, luego lo hacemos escalarmente en este eje. Llamaremos v´ a la velocidad que tiene la bola del péndulo después del choque:
Ahora tendremos la cuerda con la bola del péndulo que sale con esta velocidad. El punto crítico de la trayectoria circular será el punto superior. En este punto la bola estará sometida a su propio peso, luego necesariamente tiene que tener una aceleración. Esta aceleración tiene la dirección del radio de curvatura y está apuntando hacia el centro de curvatura, luego será la aceleración normal o centrípeta. Tendremos entonces:
siendo va la velocidad del péndulo en la parte más alta del círculo y l el radio de curvatura de la trayectoria circular.
Aplicamos ahora la conservación de la energía entre la parte más baja de la trayectoria, donde supondremos energía potencial gravitatoria nula y donde el péndulo tiene una velocidad v´, y la parte más alta de la trayectoria, en la cual la velocidad del punto es va y su altura 2l. Entonces:
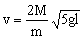
Ahora sustituimos la cuerda por una varilla de masa despreciable. Por conservación de la cantidad de movimiento entre antes y después del choque:
Después del choque la velocidad de la bola del péndulo es igual que antes. Ahora la diferencia está en que en la parte superior del círculo ahora tenemos dos fuerzas, el peso de la bola y la normal ejercida por la varilla. Ambas fuerzas tienen sentido contrario y pueden eliminarse de manera que el sumatorio de fuerzas sea nulo. De esta forma no existe aceleración normal y la velocidad en la parte superior del círculo puede ser nula. Aplicamos entonces la conservación de la energía entre la parte inferior del círculo (punto 1) donde la energía potencial gravitatoria es nula y el péndulo tiene velocidad v´, y la parte superior del círculo (punto 2) donde la altura es 2l y la velocidad es nula:
