Cuando nos encontramos en el interior de una esfera maciza (r<R), siendo la distancia al centro y R el radio de la esfera, sólo contribuyen al campo las capas de la esfera que están por debajo del radio r. Imaginemos entonces una superficie gaussiana esférica de radio r<R centrada en el centro de la esfera. Por simetría, el campo gravitatorio en todos los puntos de esta superficie gaussiana es el mismo y perpendicular a la superficie, de modo que:

g · dS=gdS

Entonces, por el teorema de Gauss:

donde M´ es la masa de esfera por debajo del radio r. Teniendo en cuenta que la densidad de la esfera es constante, y llamando M a la masa total de la esfera tendremos:

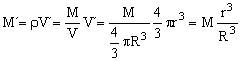
Sustituyendo:

Como puede verse, el campo es directamente proporcional a la distancia.

Si la esfera es hueca, no existe masa por debajo del radio r y el campo gravitatorio es nulo.