a) 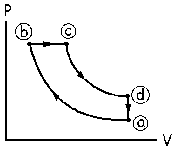
b) Vb=0.04 l, Pb=6.629·106 N/m2, Tb=994.34 K, Pc=6.629·106 N/m2, Tc=1100 K, Vc=0.044 l, Vd=0.8 l, Pd=1.143·105 N/m2, Td=344.78 K
c) Qab=0, Wab=-462.9 J, Uab=462.9 J, Wbc=26.516 J, Qbc=98.62 J, Ubc=72.104 J, Qcd=0, Wcd=500.59, Ucd=-500.59 J, Wda=0, Qda=-29.85 J, Uda=-29.85 J
a) Trazamos los ejes P-V y ponemos el punto a al azar. Lo primero que tenemos es una compresión adiabática, luego por ser compresión la presión aumenta y el volumen disminuye. Situamos el punto b de acuerdo con estas premisas y unimos los puntos a y b mediante una línea curva, que es lo que caracteriza un proceso adiabático.
A continuación tenemos que de b a c se pasa a través de un calentamiento a presión constante. De b a c por tanto se pasará a través de una línea recta paralela al eje de volúmenes (presión constante).
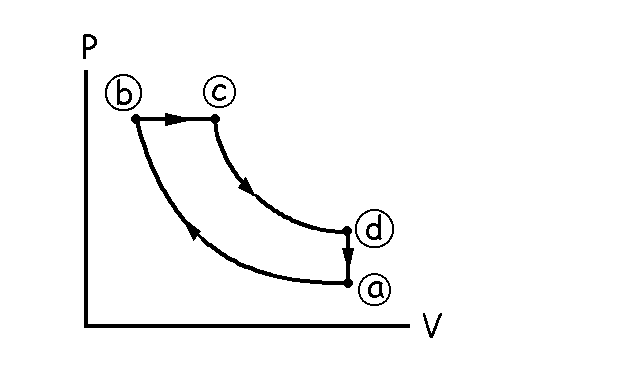 De c a d nos dicen que se pasa mediante una expansión adiabática, luego tendremos que trazar una línea curva hasta un punto en el que disminuye la presión y aumenta el volumen. Además, después el gas se enfría a volumen constante hasta llegar de nuevo al estado a, luego en los estados d y a tenemos que tener el mismo volumen, de modo que luego podamos pasar de uno a otro mediante una línea vertical en el diagrama P-V (transformación a volumen constante). El diagrama será pues el que aparece en la figura.
De c a d nos dicen que se pasa mediante una expansión adiabática, luego tendremos que trazar una línea curva hasta un punto en el que disminuye la presión y aumenta el volumen. Además, después el gas se enfría a volumen constante hasta llegar de nuevo al estado a, luego en los estados d y a tenemos que tener el mismo volumen, de modo que luego podamos pasar de uno a otro mediante una línea vertical en el diagrama P-V (transformación a volumen constante). El diagrama será pues el que aparece en la figura.
b) Conocemos las coordenadas del punto a:
Pa=105 atm
Va=0.8 l
Ta=300 K
Del punto a al punto b se pasa a través de una compresión adiabática en la que el volumen se reduce 20 veces, luego:
![]()
Vb=0.04 l
Además, como la compresión es adiabática, se debe cumplir que:
![]()
Pb=6.629 · 106 N/m2
Y también se cumplirá que:
![]()
Tb=994.34 K
Ahora de b a c pasamos a través de una transformación a presión constante, luego:
Pc=Pb=6.629 · 106 N/m2
Pc=6.629 · 106 N/m2
La temperatura en este estado la conocemos puesto que nos la da el enunciado:
Tc=1100 K
Y además la transformación es a presión constante, luego a través de la ecuación de los gases perfectos:
![]()
Vc=0.044 l
En el estado d tenemos el mismo volumen que en el estado a, luego:
Vd=Va=0.8 l
Vd=0.8 l
La transformación c—d es una transformación adiabática luego podemos aplicar la ecuación:
![]()
Pd=1.143 · 105 N/m2
Y para la temperatura tendremos la expresión:
![]()
Td=344.78 K
c) Tenemos que determinar trabajo, calor y energía interna en todas las transformaciones. Para ello necesitaremos los calores específicos a presión y a volumen constante. Conocemos la relación γ de los calores específicos, que será:
![]()
Además sabemos que para cualquier gas ideal:
![]()
Y entonces el calor específico a presión constante:
cP=γcV=1.4·2.5R=3.5R
Empezamos ahora por la transformación a—b, que es adiabática, luego:
Qab=0
Y el trabajo:
![]()
Wab=-462.9 J
Y la energía interna, a través del primer principio de la termodinámica:
Uab=Qab-Wab=-Wab=462.9 J
Uab=462.9 J
La transformación b—c es una transformación a presión constante, luego:
Wbc=PΔV=Pb(Vc-Vb)=6.629 · 106(0.044-0.04) · 10-3=26.516 J
Wbc=26.516 J
Y el calor:
Qbc=ncP(Tc-Tb)=3.5nR(Tc-Tb)
No conocemos el número de moles, pero lo podemos determinar a través de la ecuación de los gases perfectos:
![]()
Sustituyendo:
![]()
Qbc=98.62 J
Por aplicación del primer principio de la termodinámica:
Ubc=Qbc-Wbc=98.62-26.516=72.104 J
Ubc=72.104 J
La transformación c—d es adiabática luego:
Qcd=0
Y el trabajo:
![]()
Wcd=500.59 J
Y la energía interna:
Ucd=Qcd-Wcd=-Wcd=-500.59 J
Ucd=-500.59 J
Y por último, la transformación d—a es a volumen constante, luego:
Wda=0
Y el intercambio de calor:
![]()
![]()
Qda=-29.85 J
Y la energía interna:
Uda=Qda-Wda=Qda=-29.85 J
Uda=-29.85 J