a) M=7.34·10²² kg
b) v=1627.1 m/s
c) E=1.32·10¹⁰ J

a) El período en segundos será:

T=119 min=7140 s

Podemos aplicar a la órbita la tercera ley de Kepler, según la cual los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Llamaremos M a la masa de la Luna, y m a la masa del Apolo II. Entonces:

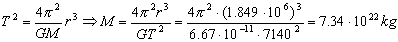
M=7.34 · 10²² kg

 

b) Tenemos que la órbita es circular. En una órbita circular el movimiento es uniforme. La única fuerza que actúa sobre el Apolo es la de atracción gravitatoria, y la única aceleración a la que está sometido es la normal o centrípeta (la tangencial es nula por ser el módulo de la velocidad constante). Como fuerza y aceleración tienen la misma dirección y sentido, aplicando la segunda ley de Newton a la dirección normal:

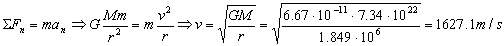
v=1627.1 m/s

 

c) La energía total en la órbita circular (energía inicial) es:

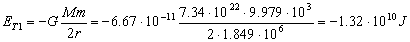
A esta energía habrá que sumarle otra, de modo que con la energía final el vehículo escape de la gravedad lunar:

E_T1+ΔE=E_T2 ⇒ ΔE=E_T2-E_T1=E_T2+1.32 · 10¹⁰

Para que el vehículo escape de la gravedad lunar habrá que situarlo en una trayectoria abierta. Existen dos trayectorias abiertas, la hipérbola y la parábola. La diferencia entre ellas es la energía; para la hipérbola la energía total es positiva, mientras que para la parábola la energía total es nula. Debemos de elegir entre una de estas órbitas. El enunciado nos dice que hay que determinar la energía mínima para que el vehículo escape de la gravedad lunar. Si nos fijamos en la expresión de esta variación de energía, es igual a un númer más la energía final. Obviamente la variación de energía será tanto menor cuanto menor sea la energía final. Entre un número positivo y cero, es menor el cero, luego habrá que transferir el vehículo a una parábola, cuya energía es nula. Tendremos entonces:

ΔE=E_T2+1.32 · 10¹⁰=0+1.32 · 10¹⁰=1.32 · 10¹⁰ J

ΔE=1.32 · 10¹⁰ J