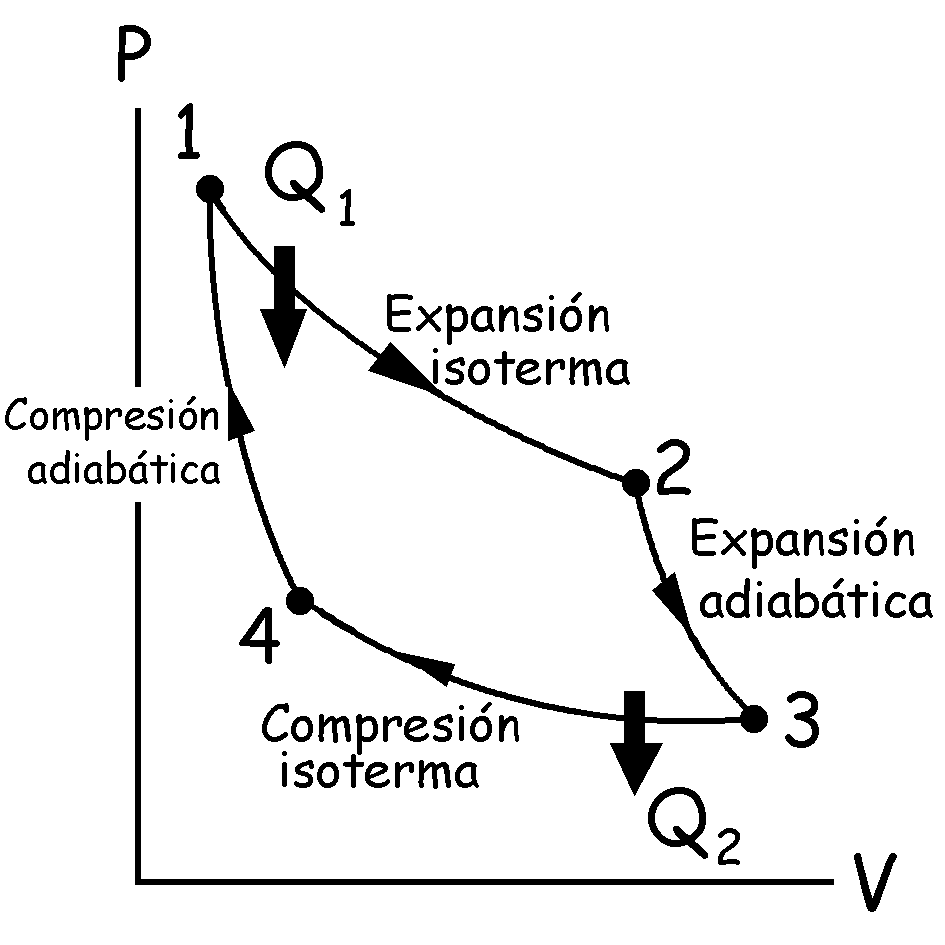
El ciclo de Carnot consiste en dos procesos isotermos y dos adiabáticos, todos reversibles, como se muestra en la figura. Los pasos serían:
1) El gas se expande isotérmicamente a temperatura T1 absorbiendo calor Q1.
2) El gas se expande adiabáticamente hasta que su temperatura baja a T2.
3) El gas se comprime isotérmicamente a temperatura T2 rechazando calor Q2.
4) El gas se comprime adiabáticamente hasta su estado inicial a temperatura T1.
Vamos a calcular la eficiencia térmica e de una máquina de Carnot.
La energía interna de un gas ideal U depende sólo de la temperatura y por tanto es constante en un proceso isotérmico. Para la expansión isoterma 1— 2:
ΔU12=0
y Q1 es igual al trabajo W12 realizado por el gas durante su expansión isotérmica a temperatura T1. Ese trabajo será:
De forma similar tendríamos en el proceso 3—4:
Como V4<V3 ⇒ Q2<0, durante la compresión isotérmica sale calor del gas a temperatura T2. La relación entre las dos cantidades de calor es por tanto:
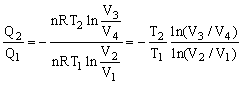
Esto puede simplificarse usando la relación T-V para un proceso adiabático. Obtenemos para los dos procesos adiabáticos:
Dividiendo la primera expresión entre la segunda tenemos:
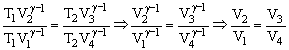
Por tanto los logaritmos de la ecuación:
son iguales y la ecuación se reduce a:
La relación entre el calor rechazado a T2 y el absorbido a T1 es igual a la relación T1/T2; entonces la eficiencia de una máquina de Carnot es:
