a) h2=0.286 m
b) vB=2.369 m/s
c) FB=6.41 N
d) θ=43.19o
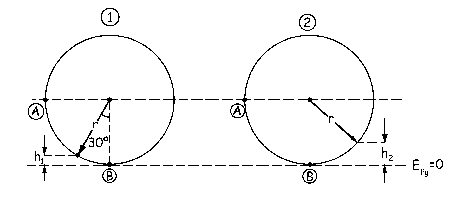
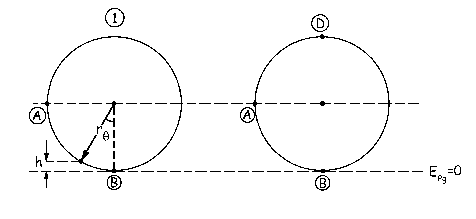
a) Aplicamos la conservación de la energía entre los estados 1, cuando se suelta el cursor con θ=30º, y 2, cuando el cursor se detiene a una altura h2 sobre el punto B. Como todas las fuerzas son conservativas:
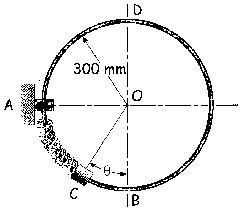
Nos dicen que el resorte tiene una longitud igual al arco AB. Cuando el cursor se encuentra en el punto C, el resorte estará comprimido, una cantidad que será la correspondiente al arco subtendido por el ángulo de 30º. Teniendo en cuenta que el arco es igual al radio por el ángulo:
Por tanto nos queda la ecuación:
h2=0.286 m
b) La energía total debe conservarse. Desde el punto 1 hasta B la velocidad debe aumentar, ya que disminuyen la energía potencial gravitatoria (disminuye la altura) y la energía potencial elástica (disminuye la deformación del resorte). Al pasar por el punto B el resorte tiene la longitud natural, luego el cursor C se separará de él y el resorte deja de actuar. Entonces empieza a disminuir la velocidad, ya que empieza a aumentar la altura, por lo que aumenta la energía potencial. La velocidad máxima entonces se alcanza en el punto B. Aplicamos la conservación de la energía entre el punto 1 (el mismo que el apartado anterior) y el punto B. Tendremos pues:
vB=2.369 m/s
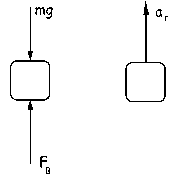c) Aislamos el cursor C en el punto B. Las fuerzas que se ejercen sobre él son la de su propio peso y la reacción de la varilla. En cuanto a aceleraciones, como el movimiento es circular tendría aceleración normal y tangencial. La tangencial es nula, ya que dicha aceleración es la derivada del módulo de la velocidad respecto del tiempo. Como el módulo de la velocidad en este punto es máximo, su derivada será nula. Sólo tenemos por tanto aceleración normal. Aplicando la segunda ley de Newton:
FB=6.41 N
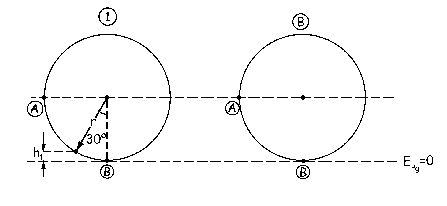
d) El cursor debe llegar al punto D. El mínimo ángulo que cumple esta condición implicará que en dicho punto la velocidad del cursor será nula (no hace falta que exista aceleración normal, ya que el peso del cuerpo puede compensarse con la normal de la varilla). Aplicamos por tanto la conservación de la energía entre el punto 1 (ángulo θ) y el punto D, donde sólo habrá energía potencial gravitatoria correspondiente a una altura de 2r:
1.98θ2+0.6615-0.6615cosθ=1.323 ⇒ 1.98θ2-0.6615cosθ=0.6615
Tenemos que resolver esta ecuación por tanteo. Vamos dando valores a θ hasta obtener el segundo miembro:
θ=0.6 ⇒ 0.166=0.6615
θ=0.7 ⇒ 0.46=0.6615
θ=0.8 ⇒ 0.8=0.6615
θ =0.75 ⇒ 0.629=0.6615
θ=0.76 ⇒ 0.6641=0.6615
θ=0.758 ⇒ 0.6572=0.6615
θ =0.759 ⇒ 0.661=0.6615
Por tanto la solución correcta es:
θ=0.759 rad=43.19º
θ=43.19º