a) v1=7555.8 m/s; T1=5829.3 s
b) hF=413 km; vF=7681.2 m/s; TF=5548.5 s
c) F=3.23·10-3 N
a) Marcaremos con el subíndice 1 a todo lo referente a la órbita inicial, y con el subíndice 2 a todo lo referenta a la órbita final. Además denominaremos con la letra M a la masa de la Tierra, y con la letra m a la masa del satélite. Para la órbita inicial tendremos:
r1=h1+R=640+6370=7010 km
Como esta órbita es circular y la única fuerza que actúa sobre el satélite es la de atracción gravitatoria, la única aceleración que tiene es la normal o centrípeta (la tangencial es nula por ser el módulo de la velocidad constante). Tanto esta fuerza como la aceleración tienen la misma dirección y sentido, luego aplicando la segunda ley de Newton:
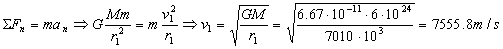
v1=7555.8 m/s
Para el período aplicamos la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores:
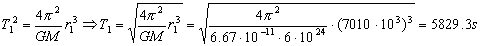
T1=5829.3 s
o bién como:
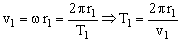
b) Como se pierden 1.4 · 105 J en cada revolución orbital y se realizan 1500 revoluciones, la energía total perdida es:
EP=1500 · 1.4 · 105=2.1 · 108 J
Y la energía inicial es:
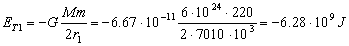
La energía final entonces será la inicial menos la que se ha perdido:
ET2=ET1-EP=-6.28 · 109-2.1 · 108=-6.49 · 109 J
Como la órbita final también es circular tendremos:
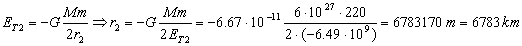
Y la altura sobre la superficie de la Tierra entonces:
r2=h2+R ⇒ h2=r2-R=6783-6370=413 km
h2=413 km
Como la órbita 2 es circular, tendremos como antes que fuerza y aceleración normal tienen la misma dirección y sentido:
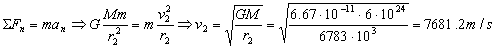
v2=7681.2 m/s
Y el período, por la tercera ley de Kepler:
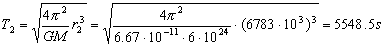
T2=5548.5 s
c) La energía perdida debe ser el trabajo realizado por la fuerza retardadora. El trabajo es el producto escalar de la fuerza por el desplazamiento de su punto de aplicación. Podemos suponer que la fuerza y el desplazamiento de su punto de aplicación se mantienen en todo momento paralelas, de modo que el trabajo será directamente el producto de la fuerza por el desplazamiento de su punto de aplicación. Para el desplazamiento, podemos realizar la aproximación de que se realizan 1500 vueltas con un radio promedio que será la media aritmética entre los radios inicial y final:
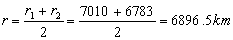
El desplazamiento entonces será el producto de las 1500 vueltas por la longitud de cada vuelta y tendremos:
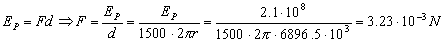
F=3.23 · 10-3 N