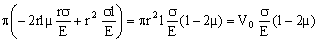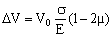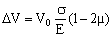
Supongamos una barra sometida a una tensión (fuerza por unidad de área) σ. Al aplicar la tensión la barra se deforma y su volumen cambia, de modo que aumenta la longitud y disminuye el radio. Si llamamos l a su longitud inicial y r a su radio inicial tendremos que la variación de volumen será:

ΔV=V_f-V₀

siendo V_f el volumen final y V₀ el inicial. Teniendo en cuenta que la barra puede tratarse como un cilindro:

ΔV=V_f-V₀=π(r+Δr)²(l+Δl)-πr²l=π(r²+Δr²+2rΔr)(l+Δl)-πr²l

Podemos despreciar los infinitésimos de orden superior a uno, ya que son términos muy pequeños en comparación con los demás:

ΔV=π(Δr²l+2rlΔr+r²Δl+Δr²Δl+2rΔrΔl)=π(2rlΔr+r²Δl)

Del módulo de Young podemos determinar el alargamiento del alambre:

Y del coeficiente de Poisson podemos determinar la variación del radio:

Sustituyendo en la expresión que nos da la variación de volumen:

ΔV=π(2rlΔr+r²Δl)=