a) Δv=225.7 m/s; Δω=10-4 rad/s; ΔT=-492.9 s; ECΔ=7·109 J; ΔEp=-0.138·1011 J;
ΔET=-6.8·109 J
b) t=5.13 días
c) n=79.6 vueltas
a) Denominaremos con el subíndice 1 a todo lo relacionado con la primera órbita, y con el subíndice 2 a todo lo relacionado con la segunda órbita. Así mismo, llamaremos con la letra M a la masa de la Tierra, y con la letra m a la masa del satélite.
Como ambas órbitas son circulares, en ellas el movimiento es uniforme. La única fuerza a que está sometido el satélite es la fuerza de atracción gravitatoria, y la única aceleración que posee es la normal (la tangencial será nula por ser el módulo de la velocidad constante). Como fuerza y aceleración tienen la misma dirección y sentido, podemos aplicar escalarmente la segunda ley de Newton. Para la órbita 1 tendremos:
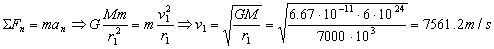
Y para la órbita 2:
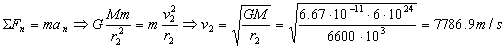
Por tanto la variación de velocidad será:
Δv=v2-v1=7786.9-7561.2=225.7 m/s
Δv= 225.7 m/s
Para la velocidad angular tenemos que el movimiento es circular uniforme luego para la órbita 1:
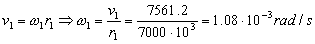
Y para la órbita 2:
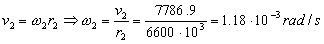
La variación en la velocidad angular es:
Δω=ω2-ω1=1.18 · 10-3-1.08 · 10-3=10-4 rad/s
Δω=10-4 rad/s
Los períodos los podemos calcular por la tercera ley de Kepler, según la cual los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes. Tendremos entonces para las dos órbitas:
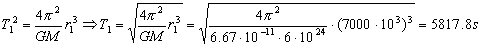
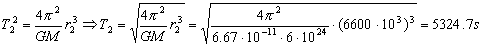
La variación en el período es:
ΔT=T2-T1=5324.7-5817.8=-492.9 s
ΔT=- 492.9 s
o bién:
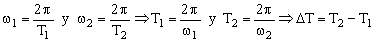
Las energías cinéticas serán en cada caso:
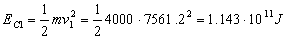
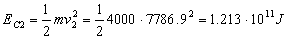
La variación por tanto:
ΔEC=EC2-EC1=1.213 · 1011-1.143 · 1011=7 · 109 J
ΔEC=7 · 109 J
Para la energía potencial:
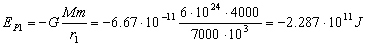
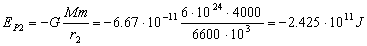
Y la variación es:
ΔEP=EP2-EP1=-2.425 · 1011+2.287 · 1011=-1.38 · 1010 J
ΔEP= -1.38 · 1010 J
Y por último para la energía total:
ΔET=ΔEC+ΔEP=7 · 109-1.38 · 1010=-6.8 · 109 J
ΔET=-6.8 · 109 J
También podríamos haber hecho:
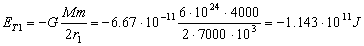
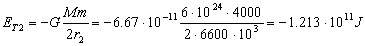
Por tanto la variación de energía total es:
ΔET=ET2-ET1=-1.213 · 1011+1.143 · 1011=-7 · 109 J
que es prácticamente lo mismo que hemos obtenido antes. También se pueden calcular las energías totales como suma de la cinética y la potencial.
b) La variación de energía total tiene que ser el trabajo realizado por la fuerza de resistencia. Dicha energía perdida será:
EP=ΔET=-6.8·109 J
que es negativa porque se pierde. El trabajo realizado por la fuerza es el producto escalar de la fuerza por el desplazamiento de su punto de aplicación. Podemos suponer que la fuerza y el desplazamiento de su punto de aplicación se mantienen en todo momento paralelas, de modo que el trabajo será directamente el producto de la fuerza por el desplazamiento de su punto de aplicación. Para el desplazamiento, podemos realizar la aproximación de que se realizan n vueltas con un radio promedio que será la media aritmética entre los radios inicial y final:

El desplazamiento entonces será el producto de las n vueltas por la longitud de cada vuelta y tendremos un modo de calcular el número de vueltas que da el satélite para perder esa energía:

Ahora, si tomamos un período promedio, que será el tiempo que tarda el satélite en dar una vuelta de 6800 km de radio, tendremos:
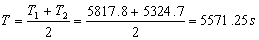
Entonces el satélite tarda 5571.25 s en dar una vuelta completa, luego en dar 79.6 vueltas tardará un tiempo t:
t=nT=79.6 · 5571.25=443346 s=5.13 días
t=5.13 días
c) El número de vueltas ya lo hemos calculado antes:
n=79.6 vueltas